締め切りに追われつつも、やはり見てしまう「たけしのコマネチ大学数学科」。今回の問題は「1辺10cmの正方形のタイルをしきつめた床に直径3cmのコインを落としたとき、4つのタイルに重なる確率は？」
もう「エクセル」はあきらめて、「Flash」で作ってみた。プレイボタンを押すと、数学研究会と同じく「1010回」コインを投げる。
第14回：アルキメデス
今回は、自らが「アキルメデスフェチ」と認める、中村亨センセが講師を務める「たけしのコマネチ大学数学科」の第14回。
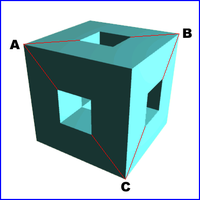問題は、「立方体の各面に垂直な方向に正四角柱の穴をあけた立体をＡ、Ｂ、Ｃの３点を通る平面で切ったとき、切り口に現れる図形を描きなさい。ただし、各穴の正方形の一辺は立方体の一辺の1/3とする」
解答図も「Shade」で描こうと思ったが（完全に「エクセル」は忘れ去られている）、老人性痴呆症のため、断念。降参です。
んで、この図形を見て、数年前、朝日新聞の1面を飾った記事を思い出した。それは「エネルギーの空中採取可能？ 電磁波を蓄える夢の宝箱開発」という記事。
なにぶん、昔の記事なので「asahi.com」には、データが残っていない。ネットで調べてみると、「おもしろ実験室《フジカット有限会社》」に記事の全文が残されていた（表示されるページの下のほう）。
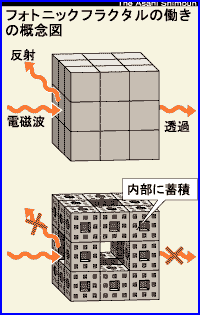記事を要約すると、フラクタルな穴のあいた立方体に電磁波を投射すると、投射をやめたあとも電磁波が1000万分の1秒ほど、内部に留まるというもの。名づけて「フォトニックフラクタル」。これが、どんなにスゴイことかというと、朝日新聞の見出しにあるように、空中からエネルギーを採取できるということ。携帯電話の充電は必要なくなるし、光だって無数のフラクタルな穴に閉じ込め、必要なときに取り出すことができる（電気を蓄える「電池」ならぬ「光池」）。と、今世紀最大の発見と、朝日新聞の1面で大々的に紹介されたのだ。
ところが、この世紀の大発見、ネットで調べてみても、その後、どうなったのかよくわからない。地道な基礎研究が進んでいるのかも知れないが、どなたか、ご存知なら教えてほしい。
「フラクタル」といえば、「コッホ曲線」や「シルピンスキーのギャスケット」が有名だが、それを立方体にしたのが、「フォトニックフラクタル」だ。フラクタル図形は、細部を取り出したときにも全体の図形と相似しているのが特徴。究極の姿を考えると、2次元なのに面積がない、立方体なのに体積がないというようなおかしなことになる。次元数を考えると、とても中途半端な次元になる、不思議な図形なのだ。朝日新聞の記事を読んでも「フォトニックフラクタル」がどのように作用しているかは、依然不明でよくわからない。ひょとして、中途半端な次元に電磁波や光が吸い込まれちゃうのかぁ～と思いたくなる。
「シルピンスキーのギャスケット」を正方形にすると、なんとなく、「曼荼羅」に似ているよね。イリア・プリゴジンは、「散逸構造」でノーベル賞を受賞した物理化学者だけど、最先端科学と東洋思想との類似性にも言及しているんだよね。この辺の話を膨らませると、竹内薫センセの「夜の物理学」という本にも言及したくなっちゃうけど、それは、またの機会に……。
じつは、私、一時期、複雑系などの「ニューサイエンス」に凝っていたときがあって、フリーになって間もなく「日経BPデジタル大事典」に「複雑系」の記事を書いたことがある。興味のある方は「ガスコン研究所（本館）」の「複雑系の話」を見てね。
McAfee(マカフィー)の摩訶不思議
先日、Windows XPパソコンが壊れた話をしたが、とりあえず、新しいパソコンを入手し、壊れたパソコンを修理に出すことにした。
で、新しいパソコンには、試用期間90日限定のウィルス対策ソフト「McAfee」が入っていた。ウィンドウズを立ち上げ、まずは使用環境を整えるため、必要最小限のソフトをインストールしたのだが、頻繁に「McAfee」の登録を促すポップアップウィンドウが開くので、ついつい登録をしてしまった。
新しいパソコンを購入したときって、それでなくても、使用環境を整えるために必要なソフトをインストールししたり、設定をしたりと、やらなければならないことが多い。そんなとき、頻繁にポップアップウィンドウが表示されるのは、非常に疎ましく迷惑だ。発売時期から、それほど経っていないパソコンなのに「Adobe Reader」は、バージョンアップを促され、しかも「7.03」「7.05」「7.07」と小刻みに差分をロードし、その都度、再起動を求める始末だ。
システムは、ウィンドウズを初めて起動した日や、再起動した回数を記録しているはず。そこで、少しでもユーザーのことを思うのなら、初起動から１週間、再起動が10回を超えるまでは、バンドルソフトのインストールや登録を促さないようにできないものか。それでなくても、新しいパソコンを購入する動機が、それまで使っていたパソコンが起動できなくなったからという場合、長年連れ添った妻から、突然、離婚届を付き尽きられたようなもので（離婚経験はないが）、暗澹たる気持ちで、なんでこんなときに……と精神的には、いっぱい、いっぱいになっているのよ。
そんなわけで「McAfee」を登録したら、返信メールがブロックされて、相手に送信されない現象が起きた（もちろん、ウィルスに感染したメールを送信しようとしたわけではないよ）。もうパニック状態で「アプリケーションの追加と削除」で「McAfee」を削除しようとしたら、ちゃんとアンインストールプログラムを使っているにもかかわらず、プログラムを削除することができない。ネットで調べると、ソースネクストのページに「McAfee のアンインストール方法」が載っていた。どうやら、アンインストールする順番が重要らしい。特定の順番でアンインストールしていかないと削除できないのだ。自社のアンインストールプログラムで安全かつ確実にアンインストールできないウィルス対策ソフトって、いかがなものか。 他社のホームページでアンインストールの方法を紹介してもらっているというのも、どーなのよ？ 「McAfee」といえば、今年、3月にマイクロソフトの「エクセル」をウィルスと誤認する騒ぎがあったばかりだし……。
ソースネクストのホームページで「McAfee のアンインストール方法」を載せているのも、ソースネクストのウィルス対策ソフトを購入したユーザーが「McAfee」のアンインストールができないという問い合わせが多かったためではないかと考えてしまう。
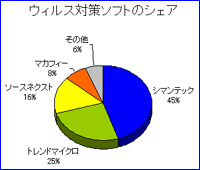ソースネクストは、この7月にウィルス対策ソフトのバージョンアップ、年間更新料を無料にした「ウイルスセキュリティZERO」を発売した。こういうご時勢だから、ウィルス対策ソフトは必須だが、期限切れのメッセージがわずらわしい。毎年、更新料を払い続けるのもつらいところ。3,970円で、Windows Vistaの公式サポート期間が終了する2016年まで、更新料なしで使い続けることができるのは、いいかも。
 ウイルスセキュリティZERO (説明扉付きスリムパッケージ版) 販売元：ソースネクスト |
第13回：ソファー問題
去年の12月に購入したばかりのパソコン(Windows XP)が壊れた。リカバリーもできないことから、ハードウェアのどこかが壊れた可能性がある。こうなるとお手上げだ。使用期間、半年ちょっとで、なんで壊れるのかなーと、かなりヘコんだ状態で「たけしのコマネチ大学数学科」を見る。
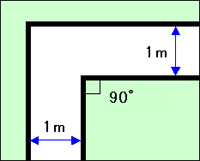まずは例題「図のような直角に曲がった幅１ｍの通路で運ぶことのできる長方形のソファーの最大面積を答えなさい」
コマ大数学研究会の面々が体を張って出した答えが「0.98」平方メートル。そこへマス北野が「１ｍ×１ｍの正方形でも、それより大きい」と、するどい突っ込みが入った。
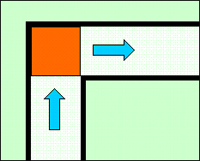これに対してコマ大数学研究会の面々は、「１平方メートルまではいきませんよね」と、竹内薫センセに助けを求めるが、「数学的には入るということで…」と薫センセも困惑ぎみだ。「引越し屋さん的には、そうはいきません」ダンカンの言うとおり、現実的には、１ｍの通路に１ｍの幅のソファーを通せと言われても、引越し屋としてはコマってしまうだろう。必ず「余裕」、「遊び」が必要だ。
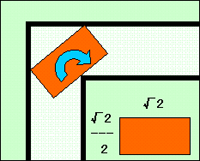それはともかく、長方形の場合も、面積は１平方メートルになるとのこと。
さて、これを踏まえ、今回の問題は「この１ｍ幅の通路を通ることのできる最大のソファーの形は？」
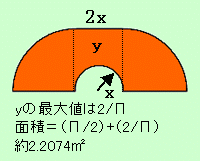
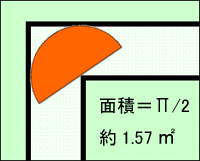東大生の解答は、円を半分にした形。面積は「Π/2」で約1.57平方メートル。マス北野は、角を曲がりやすくするため、ヘコみを入れると、さらに面積の大きなソファーを通すことができることまで気が付いたが、具体的な形、最大面積までは出すことができなかった。結論から言うと受話器のような「ハマースレー型」になるらしい。
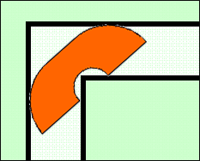数学的なことはともかく、このヘンテコな形をしたソファーが１ｍ幅の直角の通路をすり抜ける様を見せられたら納得するしかない。さらに「ハマースレー型」の角を少し丸めた「ガーバー型」もあるらしい。
通路の壁に沿って90度回転する「ハマースレー型」のソファーを見て、マス北野は「ロータリーエンジンみたいな動き」と称したが、興味のある人は、Wikipedia「ルーローの三角形」と「式から求めるトロコイド曲線 ～オニギリ・ジョーPresents～」のサイトが参考になるかも。もっとも、数式の部分は、私には難しすぎて理解しようという気にもなれず、ビジュアルを眺めただけだが……。
ところで、竹内薫センセの「ビジュアル式 数学嫌いが治る本」を読んだ。副題に「絵で考えると、面白いほどわかる」とある。この本は、「ルーレットとモンテカルロ法」（確率入門）から始まり、「サイン・コサイン・タンジェント」（三角関数）や「微かに分けたり積み重ねたり」（微分積分入門）といった章に分かれていて、「数学オチこぼれ」の私にもわかりやすいように、難しい数式よりもビジュアルを多用して説明してくれている。「なるほど、そうだったのか」と唸りながら読み進めた。途中「コマネチ大学数学科」の第５回「ケプラー予想」の問題も登場する。
で、この本には、じつは大きな野望が秘められている。それは、「数学嫌い」を治すだけでなく、最終的に、今、株価分析などで話題を呼んでいる「ブラック・ショールズ方程式」を理解させるところまで、私たちを連れて行こうという無謀とも言える試みだ。モンテカルロ法も三角関数も微分積分も、そのための伏線、一歩ずつ登る階段なのだ。
「数学オチこぼれ」の私にとって「微分積分」は難関中の難関。よく「微分はグラフの傾き」、積分は「グラフの面積」を求めると書かれているが、意味としてはわかるのだが、いまいち感覚的に「わかった！」とは、言い難かった。本書は「文科系ビジネスマン？」を対象にしているので、微分は「売上」の「前年度比」と説明している。もちろん「前月比」、「前日比」と微分していくことが可能だ。一方、積分は「前日比」、「前月比」を積み上げていくと「総売上」になるという説明をしている。「なるほど～」とわかった気になる。
ビジュアル的に解釈すれば、デジカメ写真をどんどん拡大（ズームイン）していけば、ドットのギザギザが見えてくる。これが「微分」で、逆にズームアウトしていけば、滑らかに見える。これが積分だ。
たとえば、第10回の「トイレットペーパー」でトイレットペーパーに切り込みを入れ、それを展開して台形にすることで、その断面積を求め、トイレットペーパーの厚みや巻き数を求める問題だって、細かく見ると、トイレットペーパーの厚み分の段差（ギザギザ）があるはず。そこには微分積分という考え方が入っているはず（間違っていませんよね？＞竹内薫センセ）。
本書で竹内薫センセは、とりあえず「紙と鉛筆を使って計算してみる」ということを力説している。難しい数式を「難しい」とあきらめて、何もしなかったら、何も生まれず、何も理解を得られない。
私は本書を読み通した（つまり眺めた）だけで、まだ何も実践をしていないので大きいことは言えない。でも、いつか「エクセル」で「ブラック・ショールズ方程式」を使って株価分析に挑戦してみたいと思う。そのとき、あらためて、本書を再度、紹介したい。
最後に本書を読んで、「へぇ～そうなのか！」と驚いたこと。それは「勾配」に関すること。よく道路や鉄道で勾配率を表す「５％」といった標識があるよね。この「勾配率」なんだけど、じつは角度「45度」を勾配「100％」と表記するのを知った。tan(45度)=1、=100％だからだ。
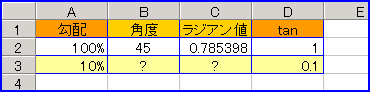
で、本書の受け売りだが「勾配率100％は45度、では勾配率10％は、角度に変換すると何度か？」という問題。勾配率100％が45度だから、その1/10で「4.5度」という答えは、性急すぎて竹内薫センセの「思うツボ」にはまってしまう。要は「tan（？）が「0.1」になればいいはずだ。「エクセル」を使って、結果から逆計算してみよう。
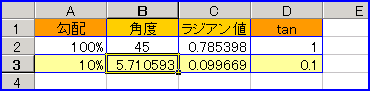
tan(45度)が「1」、つまり「100％」になる。エクセルでは、引数の角度はラジアン値で指定するので、セルC2は「=radians(45)」として、ラジアン値を求める。セルD2は「=tan(C2)」とする。すると「1」になるわけ。
勾配が「1/10」になるということは「tan(ラジアン値)」が「0.1」になるということなので、このときのラジアン値を求めるには、タンジェントの逆数、アークタンジェント「=ATAN(D3)」とする。さらに、このラジアン値を角度に変換するには「=DEGREES(C3)」で、結果は「4.5度」ではなく、約「5.71度」になる。
というわけで、Windows XP（Office 2003)が壊れてしまったので、普段、あまり使っていないWindows 2000（Office 2000）で作成した……；；
 ビジュアル式 数学嫌いが治る本 著者：竹内 薫 |
言葉の力
今ワールドカップで現役引退するジダンをおちょくるつもりは毛頭ない（頭に毛がないという意味ではない、いや、もともとはそういう意味か…）。ロッカールームに引き上げたジダンが地団駄踏んで、蹴飛ばしたドアは永久保存するそうである。
しかし、ワールドカップの決勝戦、しかも、自身の引退試合をかけて、ジダンがキレてしまった言葉とは……。あのときマティラッティ選手にどんな言葉を投げかけられたのか、気になるところだ。「極めて深刻な言葉」を投げかけられたとし、一部報道によると「人種差別」的な言葉を言われたとか、言われてないとか……。
で、私の興味を引いたのは、移民が多いフランスが抱える人種問題や、イタリアチームの八百長疑惑など、さまざまな取り巻く情勢ではない。ワールドカップの決勝戦、自らの引退試合という、極めて重要な場面でジダンをキレさせた「言葉の力」だ。たったひとつの「言葉」がワールドカップ決勝戦の行方、ひとりのサッカー選手の有終を左右してしまうこともあるのだ。
私の好きな映画のひとつに「羊たちの沈黙」がある。クラリス（ジョディー・フォスター）がレクター博士（アンソニー・ホプキンス：たんなる殺人犯としてでなく、危険な「人食いハンニバル」として厳重に収監されている）の独房を訪れ、一連の連続殺人のヒントを得ようとする場面のあと、立ち去るクラリスに対して、レクターの隣の房にいる囚人が自分の精液を投げかけてクラリスを陵辱するシーンがある。
次にクラリスがレクターの元を訪れるときは、隣の房の囚人は、すでにいない。夜毎というか、レクター博士がその囚人に言葉をささやき続け、それに耐えきれずにその囚人は自殺したのだという。もちろん、具体的にどんな言葉をささやいたのかは、映画の中では説明されていない。
一時の興奮状態の結果としても、人を自殺に追い込むような「言葉」とは、いったいどんな言葉だったのだろうか。想像してみても、たぶん個人的な事柄だろうから、わかるはずもない。「羊たちの沈黙」のハンニバル・レクター博士の「言葉」が、マティラッティ選手の発した言葉以上に、ずっと気になっている……。
 |
 |
羊たちの沈黙 アルティメット・コレクション
販売元：ソニー・ピクチャーズエンタテインメント |
ボーダフォンの予想外な動き？
ボーダフォンの「AQUOSケータイ905SH」など、シャープ製の一部機種で「みられまくっちゃ」と入力するとフリーズする現象が報告されている。ドコモの「SH902i」や「SH902i」でも同様の現象が発生するらしい。「ふられまくっちゃ」や「おこられまくっちゃ」と入力してもフリーズするという報告もある。フリーズすると電源ボタンも反応しなくなるので、電池パックを外すしか対処の方法がないようだ。詳しくは以下のブログを参照してほしい。
第12回：1000
いつものように「たけしのコマネチ大学数学科」の番組が始まる頃は、すっかり酔っ払って「へべれけ」になっていた。その日のTBS「日本語王」という番組で「へべれけ」の語源はギリシャ語の「ヘーベーエリュエケ」で「ヘーベーのお酌」という意味だと、学者の人（名前忘れた）が言っていた。手元に「トリビアの泉」のボタンがあったら「へえ～へぇ～へぇ～」と12回くらい押していただろう。ところが「日本語王」に異議を唱えているのが「豆知識王」だ。
「へべれけ」論議はともかく、今回の問題は「1～1000の数字が振られている1000個の電球がある。すべてOFFの状態の始めて、１の倍数、２の倍数、３の倍数……1000の倍数まで該当する電球のON、OFFを切り替えていくと最後に点灯している電球は何個か？」
とりあえず、1～10の電球で試してみると「10」までいったとき、点灯しているのは「1」、「4」、「9」番の電球ということになる。
これは、たとえば「6」の約数を考えると「1、2、3、6」で、約数の数が偶数のときは、ON、OFF、ON、OFFときて「OFF」で終わっちゃう。「9」の約数「1、3、9」のように約数の数が奇数の場合のみON、OFF、ONで「ON」で終わる。つまり電球が点灯したままになる。
で、約数の数が奇数になる状態というのは「4=2×2」や「9=3×3」のように、約数で割った答えが約数と同じ数、つまり平方になっている場合だ。
いつも体を張って難問に挑む「コマ大数学研究会」の面々だが、今回は「米粒」に1～1000までの数字を書き、ON、OFFの代わりにひっくり返していくという手法をとった。番組内では「コマ大」ならぬ「コメ大」だと揶揄されていたが、論より証拠、実証が大事だ……「米百俵」という言葉があるが、今回は「米千粒」の心意気だ。
私も「エクセル」で検証。セルA1に「1」と入力。「編集」メニューの「フィル」から「連続データの作成」をクリック。範囲に「列」を選び、停止値を「1000」にして「OK」ボタンをクリック。
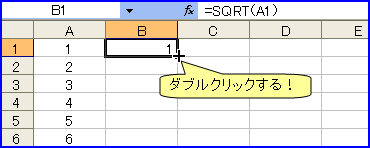
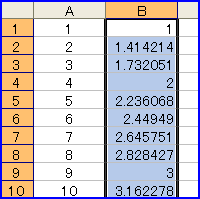セルB1に「=SQRT(A1)」と入力（SQRTは平方根を求める関数）。セル枠の右下隅にカーソルを合わせると「＋」マークになるので、ダブルクリックする。 「エクセル」は、一瞬で1～1000までの平方根を表示する。で、このうち解が整数になっている数を数えればよい。
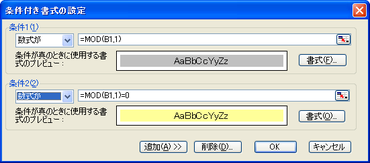
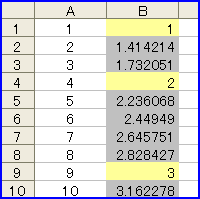条件付き書式で整数の場合と、そうでない場合を色分けしてみよう。「MOD」は、割り算の余りを求める関数。数値を「1」で割って、余りが出なければ「整数」ということになる。
というわけで「コメ大数学研究会」と同レベルだが「31個」という正解にたどりついた。めでたし、めでたし。
Google Earth Weather Tools
昨日は、北朝鮮がスカッドやノドンやテポドン２のミサイルを計７発も発射したというニュースで埋め尽くされた。繰り返し流される「テポドン」の発射シーンと、舞水端里（ムスダンリ）にあるミサイル発射台の衛星写真だ。
折りしも、7月4日はアメリカの独立記念日で、1年ぶりにスペースシャトル「ディスカバリー」が発射された。スペースシャトルから夜の日本を眺めると、光の点が見事に日本列島の形になって見えると、宇宙飛行士の毛利さんも実体験を語っていた。
夜の衛星写真を見ると、日本列島はくまなく光にあふれ、列島の形がはっきりわかる。それは韓国も同じだ。ところが北朝鮮は電力不足で、そこだけが、すっぽり、闇に包まれている。
何も知らされていない北朝鮮の人たちに、この衛星写真を見せれば、自分たちが置かれている状況が一目瞭然だろう。
ところで、7月3日の「Google Earth Blog」で、いくつかのツールを集めた「Weather Tools」が公開された。「Google Earth」を組み込んでいる人なら、上記Blogから、「weather and tracking tools network link」をクリックするだけで表示される。「Temporary Places」にダウンロードされるので、あとは「My Places」などのフォルダに保存すればよい。
この中で私が待ち望んでいた機能が「Global Cloud Map」と「Real-Time Day and Night Earth」だ。
「Global Cloud Map」は、地球を覆う「雲」の衛星写真をマッピングしたもの。リアルタイムとはいかないが、一定の間隔で最新情報に更新される（※画面は、昨夜9時頃のキャプチャだが、台風3号の影響で日本列島を雨雲が覆っている。台風の進路なども表示させることができる）。
「Real-Time Day and Night Earth」は、地球の昼の部分と夜の部分をリアルタイムで表示するもの。もちろん、たんに「Google Earth」の画像に光のあたっている部分と影の部分をオーバーレイしているにすぎないが、このふたつの機能を組み合わせると、宇宙空間から地球を眺めている気分になれる。
スッキリしたときの快感
クルマのナンバープレートの4桁の数字や鉄道の切符の4桁の数字を四則演算で「10」にするという遊びがあるよね「算数・数学が得意になる本
４つの数字を使って四則演算をし、たとえば10になるような数式を頭の中で探してみるのです（カッコの使用も可）。試しに１、１、９、９を使って10になる式を作ってみてください。
算数・数学が得意になる本
「数学落ちこぼれ」の私が、つい最近「算数・数学が得意になる本」（芳沢光雄・著）を読んだ。帯に「つまずいても大丈夫！」と書かれていたからだ。
この本は、算数、数学の授業の中で、どこで「つまずき」やすいのか、「つまずく」原因を丹念にわかりやすく説明し、その「つまずき」を解消してくれる。
また、おもしろい数学クイズ、数学にまつわるおもしろ話としても読むことができる。
おもしろ数学クイズの例──。
【問題】太郎君だけで行うと10日間かかり、花子さんだけで行うと15日間かかる仕事があります。この仕事を太郎君と花子さんの２人で行うと、何日間で終わりますか。
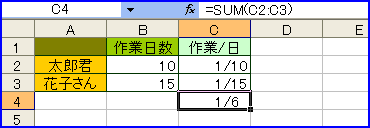これは小学校の問題。ポイントは、仕事全体を１として、１日あたりの仕事の進み具合を「分数」で表すこと。分数の足し算でふたりの１日あたりの仕事量が「1/6」になるので「6日間」で仕事が終わることがわかる。
【問題】行きは時速30kmで走り、帰りは時速60kmで走る自動車があります。その自動車の往復の平均速度を求めなさい。
ついつい、(30＋60)÷2として、平均時速「45km」としてしまいがち。平均速度は、距離÷時間なので、たとえば、目的地までが60kmの場合なら……。
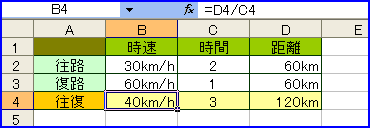となるわけ。もちろん、目的地までの距離を変えても結果は同じ。
次におもしろ話の例──。
割合を表す0.01を1％と書くことはよいとして、0.1を1割、0.01を1分、0.001を1厘で書くことに関して、注意しなくてはならないことがあります。それは「九分九厘成功する」というときは「99％成功する」という意味だからです。
50数年生きてきて、指摘されるまで気がつかなかったよ。「九分九厘成功する」は、文字通りに受け止めれば「9割がた失敗する」ってことじゃないか! 芳沢光雄氏によると、江戸時代の算術の教科書『大全塵劫記』に小数の説明があって「分、厘、毛」と並んでいるが「割」はない。「割」はあとから割り込んできた概念なのだとか……。
ちなみに「エクセル」で小数を「○割○分○厘」と表示するには、このようにする。意外とどの「エクセル」本にも載っていないんだよね（野球の打率を計算するときぐらいしか、必要性がないせいかも；；）。
というわけで、おもしろく読み進み、第3部、高校数学の「つまずき」に入ると、一度読んだくらいでは理解できなくなった。三角関数、順列、帰納法、ベクトル、行列……。「行列」と聞いても「行列のできるラーメン店」くらいしか思い浮かばないよー（オヤジ臭が;;）。そして、最後に控えしは「微分積分」。
でも、芳沢光雄氏は「つまずいても大丈夫！」と励ましてくれる。あきらめずにがんばろう。
 算数・数学が得意になる本 著者：芳沢 光雄 |