ヒッチコックの「北北西に進路を取れ」ではなく、「東北東に進路を取れ」の「たけしのコマ大数学科」
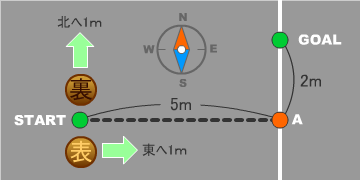
問題:南北の方向に引いてある白線上の点Aから西へ5mの点でコインを投げ、表が出たら東へ1m、裏が出たら北へ1m進みます。白線に達するまでこれを続けたとき、点Aから2m北の点に達する確率を求めなさい。
※1982年 京都大学(理系)入試問題を参考

What are you studying?
ヒッチコックの「北北西に進路を取れ」ではなく、「東北東に進路を取れ」の「たけしのコマ大数学科」
問題:南北の方向に引いてある白線上の点Aから西へ5mの点でコインを投げ、表が出たら東へ1m、裏が出たら北へ1m進みます。白線に達するまでこれを続けたとき、点Aから2m北の点に達する確率を求めなさい。
※1982年 京都大学(理系)入試問題を参考

国立大学に挑戦シリーズ第2弾。名古屋大学(名大)は、ノーベル賞やフィールズ賞の受賞者を輩出している名門の大学だ「たけしのコマ大数学科」
問題:3x+2y≦2008を満たす、0以上の整数の組(x,y)の個数を求めよ。
※名古屋大学(理系)前期 入試問題
上は、3x+2y≦18としたときの図。x≧0, y≧0と、この式に囲まれた部分に整数の格子点が何個あるかとゆーことね^^; ステッパーの数値を変えると、格子点の数を計算するようにしたけれど、グラフは変わらない><;
問題:ある駅前の土地が競売によって売り出されることになった。競売の方法は以下の通り。
買い手は自分の買い値を紙に記入して、それを秘密にしたまま、入札箱に投入するものとする。買い手が入札を終えた後、売り手は入札箱を開けて一番高い値をつけた買い手に、その人がつけた買い値でこの土地を売ることにする。一番高い買い値をつけた買い手が複数いる場合は、その中から公平なくじ引きで選ばれた1人に売ることにする。
A氏は、この土地を用いた事業を行うことで5億円の利益が得られるとする。つまり、競売に参加してX億円で土地を買うことができたとすると、A氏の利益は5-X億円になる。土地を変えなかった場合は、事業の利益も土地購入代も発生しないので、A氏の利益は0円と考える。
この競売に、A氏の他にもう一人の買い手(B氏)が参加しているとする。買い値は、1億円単位でつけなければいけないものとする。B氏のつける買い値をY億円とし、Yは1から10までの整数を等しい確率でとるものとする。
利益の期待値を最大にするためには、A氏はいくらの買い値をつければ良いか。
※2010年東京大学(後期)総合科目II問題
この土地が生みだす利益は5億円なので、5億円で落札しても利益は「0円」。利益を生む入札額は「1~4億円」となるが、相手より額が大きくなければ落札できない。さて、もっとも利益を期待できる入札額は……。
爺は、蟻とか、蜂とかの「群れとしての行動」にすごく興味がある。やつらは、個体としては、それほど考えているとは思えないのだが、集団になると、集団の中の自分の役割を見つけ、秩序が生まれ、まるで、集団が意思を持ったような「群行動」を取る。
上のFlashは、、単純な線で「小魚」をイメージしたものだが、群行動の数理モデルを適用すると、なんとなく、小魚のように見えなくもない^^; ここで言う「群行動」とは、どんなものなのか?
今回は、東大入学率日本一、数学オリンピックでも数多くのメダリストを輩出しているという、筑波大学付属駒場高校(筑駒)の入試問題に挑戦「たけしのコマ大数学科」
問題:1辺の長さが12cmの立方体の容器に11cmの深さまで水が入っています。この容器には、ふたがついていて回転しても水はこぼれないものとします。点Gを通り、4点A,E,G,Cを含む平面に垂直な直線を「l」とし、lを軸として容器を回転します。点Eが水面上に来るとき、水面の面積を求めなさい。
※筑波大学付属駒場高校入試問題
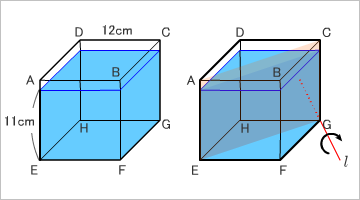
lを軸として回転させるとき、右回りと左回りが考えられるが、中村亨センセから「今回は、向かって右回りで考えてほしい」との注釈がついた。
トリコロールといえば、フランス国旗。青は自由、白は平等、赤は博愛という意味があるらしい。床屋さんの店先でくるくる回る看板燈も、青、白、赤のトリコロールだが、赤は血管の動脈、青は静脈、白は包帯を表しているという。いったい、今回はどんな問題なの「たけしのコマ大数学科」。
問題:赤色の島、青色の島、黄色の島がそれぞれちょうど3つずつある。これらの島に次の2条件を満たすようにいくつかの橋を架ける。
条件(1):どの2つの島も、1本の橋で結ばれているか、結ばれていないかのいずれかであって、橋の両端は相異なる2つの島に繋がっている。
条件(2):同色の2つの島を選ぶと、その2つの島は橋で直接結ばれておらず、その2つの島の両方と直接結ばれている島も存在しない。
橋の掛け方は何通りあるか。ただし、1本も橋をかけない場合も1通りと数える。
※2010年 日本数学オリンピック予選問題
たぶん、問題解決には役に立たないだろうけれど、いちおうFlashを作成した。島と島をクリックすると橋(線)で結ばれる。問題は、橋を何本架けられるかではなく、何通りの架け方があるかなので注意してね。また、爺の趣向で島の色は勝手に変えさせてもらったよ^^;