去年の12月に購入したばかりのパソコン(Windows XP)が壊れた。リカバリーもできないことから、ハードウェアのどこかが壊れた可能性がある。こうなるとお手上げだ。使用期間、半年ちょっとで、なんで壊れるのかなーと、かなりヘコんだ状態で「たけしのコマネチ大学数学科」を見る。
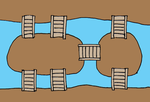
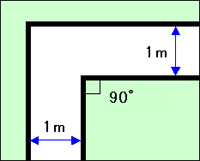 まずは例題「図のような直角に曲がった幅1mの通路で運ぶことのできる長方形のソファーの最大面積を答えなさい」
まずは例題「図のような直角に曲がった幅1mの通路で運ぶことのできる長方形のソファーの最大面積を答えなさい」
コマ大数学研究会の面々が体を張って出した答えが「0.98」平方メートル。そこへマス北野が「1m×1mの正方形でも、それより大きい」と、するどい突っ込みが入った。
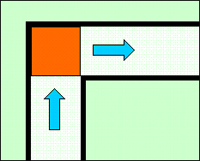 これに対してコマ大数学研究会の面々は、「1平方メートルまではいきませんよね」と、竹内薫センセに助けを求めるが、「数学的には入るということで…」と薫センセも困惑ぎみだ。「引越し屋さん的には、そうはいきません」ダンカンの言うとおり、現実的には、1mの通路に1mの幅のソファーを通せと言われても、引越し屋としてはコマってしまうだろう。必ず「余裕」、「遊び」が必要だ。
これに対してコマ大数学研究会の面々は、「1平方メートルまではいきませんよね」と、竹内薫センセに助けを求めるが、「数学的には入るということで…」と薫センセも困惑ぎみだ。「引越し屋さん的には、そうはいきません」ダンカンの言うとおり、現実的には、1mの通路に1mの幅のソファーを通せと言われても、引越し屋としてはコマってしまうだろう。必ず「余裕」、「遊び」が必要だ。
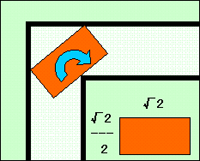 それはともかく、長方形の場合も、面積は1平方メートルになるとのこと。
それはともかく、長方形の場合も、面積は1平方メートルになるとのこと。
さて、これを踏まえ、今回の問題は「この1m幅の通路を通ることのできる最大のソファーの形は?」
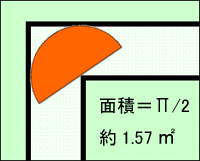 東大生の解答は、円を半分にした形。面積は「Π/2」で約1.57平方メートル。マス北野は、角を曲がりやすくするため、ヘコみを入れると、さらに面積の大きなソファーを通すことができることまで気が付いたが、具体的な形、最大面積までは出すことができなかった。結論から言うと受話器のような「ハマースレー型」になるらしい。
東大生の解答は、円を半分にした形。面積は「Π/2」で約1.57平方メートル。マス北野は、角を曲がりやすくするため、ヘコみを入れると、さらに面積の大きなソファーを通すことができることまで気が付いたが、具体的な形、最大面積までは出すことができなかった。結論から言うと受話器のような「ハマースレー型」になるらしい。
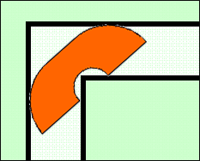 数学的なことはともかく、このヘンテコな形をしたソファーが1m幅の直角の通路をすり抜ける様を見せられたら納得するしかない。さらに「ハマースレー型」の角を少し丸めた「ガーバー型」もあるらしい。
数学的なことはともかく、このヘンテコな形をしたソファーが1m幅の直角の通路をすり抜ける様を見せられたら納得するしかない。さらに「ハマースレー型」の角を少し丸めた「ガーバー型」もあるらしい。
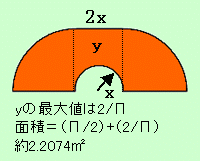 通路の壁に沿って90度回転する「ハマースレー型」のソファーを見て、マス北野は「ロータリーエンジンみたいな動き」と称したが、興味のある人は、Wikipedia「ルーローの三角形」と「式から求めるトロコイド曲線 ~オニギリ・ジョーPresents~」のサイトが参考になるかも。もっとも、数式の部分は、私には難しすぎて理解しようという気にもなれず、ビジュアルを眺めただけだが……。
通路の壁に沿って90度回転する「ハマースレー型」のソファーを見て、マス北野は「ロータリーエンジンみたいな動き」と称したが、興味のある人は、Wikipedia「ルーローの三角形」と「式から求めるトロコイド曲線 ~オニギリ・ジョーPresents~」のサイトが参考になるかも。もっとも、数式の部分は、私には難しすぎて理解しようという気にもなれず、ビジュアルを眺めただけだが……。
ところで、竹内薫センセの「ビジュアル式 数学嫌いが治る本」を読んだ。副題に「絵で考えると、面白いほどわかる」とある。この本は、「ルーレットとモンテカルロ法」(確率入門)から始まり、「サイン・コサイン・タンジェント」(三角関数)や「微かに分けたり積み重ねたり」(微分積分入門)といった章に分かれていて、「数学オチこぼれ」の私にもわかりやすいように、難しい数式よりもビジュアルを多用して説明してくれている。「なるほど、そうだったのか」と唸りながら読み進めた。途中「コマネチ大学数学科」の第5回「ケプラー予想」の問題も登場する。
で、この本には、じつは大きな野望が秘められている。それは、「数学嫌い」を治すだけでなく、最終的に、今、株価分析などで話題を呼んでいる「ブラック・ショールズ方程式」を理解させるところまで、私たちを連れて行こうという無謀とも言える試みだ。モンテカルロ法も三角関数も微分積分も、そのための伏線、一歩ずつ登る階段なのだ。
「数学オチこぼれ」の私にとって「微分積分」は難関中の難関。よく「微分はグラフの傾き」、積分は「グラフの面積」を求めると書かれているが、意味としてはわかるのだが、いまいち感覚的に「わかった!」とは、言い難かった。本書は「文科系ビジネスマン?」を対象にしているので、微分は「売上」の「前年度比」と説明している。もちろん「前月比」、「前日比」と微分していくことが可能だ。一方、積分は「前日比」、「前月比」を積み上げていくと「総売上」になるという説明をしている。「なるほど~」とわかった気になる。
ビジュアル的に解釈すれば、デジカメ写真をどんどん拡大(ズームイン)していけば、ドットのギザギザが見えてくる。これが「微分」で、逆にズームアウトしていけば、滑らかに見える。これが積分だ。
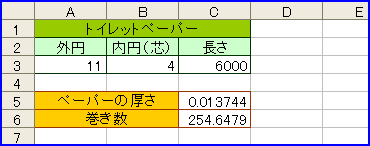
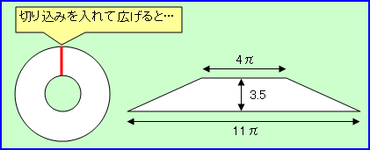
たとえば、第10回の「トイレットペーパー」でトイレットペーパーに切り込みを入れ、それを展開して台形にすることで、その断面積を求め、トイレットペーパーの厚みや巻き数を求める問題だって、細かく見ると、トイレットペーパーの厚み分の段差(ギザギザ)があるはず。そこには微分積分という考え方が入っているはず(間違っていませんよね?>竹内薫センセ)。
本書で竹内薫センセは、とりあえず「紙と鉛筆を使って計算してみる」ということを力説している。難しい数式を「難しい」とあきらめて、何もしなかったら、何も生まれず、何も理解を得られない。
私は本書を読み通した(つまり眺めた)だけで、まだ何も実践をしていないので大きいことは言えない。でも、いつか「エクセル」で「ブラック・ショールズ方程式」を使って株価分析に挑戦してみたいと思う。そのとき、あらためて、本書を再度、紹介したい。
最後に本書を読んで、「へぇ~そうなのか!」と驚いたこと。それは「勾配」に関すること。よく道路や鉄道で勾配率を表す「5%」といった標識があるよね。この「勾配率」なんだけど、じつは角度「45度」を勾配「100%」と表記するのを知った。tan(45度)=1、=100%だからだ。
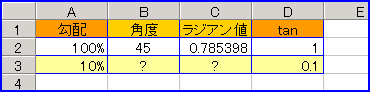
で、本書の受け売りだが「勾配率100%は45度、では勾配率10%は、角度に変換すると何度か?」という問題。勾配率100%が45度だから、その1/10で「4.5度」という答えは、性急すぎて竹内薫センセの「思うツボ」にはまってしまう。要は「tan(?)が「0.1」になればいいはずだ。「エクセル」を使って、結果から逆計算してみよう。
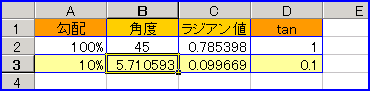
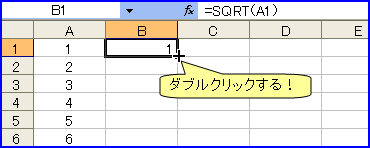
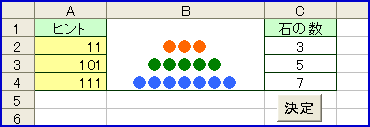
tan(45度)が「1」、つまり「100%」になる。エクセルでは、引数の角度はラジアン値で指定するので、セルC2は「=radians(45)」として、ラジアン値を求める。セルD2は「=tan(C2)」とする。すると「1」になるわけ。
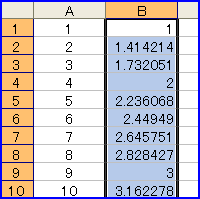
勾配が「1/10」になるということは「tan(ラジアン値)」が「0.1」になるということなので、このときのラジアン値を求めるには、タンジェントの逆数、アークタンジェント「=ATAN(D3)」とする。さらに、このラジアン値を角度に変換するには「=DEGREES(C3)」で、結果は「4.5度」ではなく、約「5.71度」になる。
というわけで、Windows XP(Office 2003)が壊れてしまったので、普段、あまり使っていないWindows 2000(Office 2000)で作成した……;;
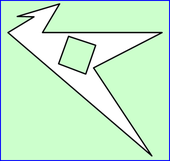
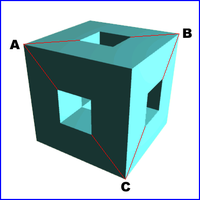 問題は、「立方体の各面に垂直な方向に正四角柱の穴をあけた立体をA、B、Cの3点を通る平面で切ったとき、切り口に現れる図形を描きなさい。ただし、各穴の正方形の一辺は立方体の一辺の1/3とする」
問題は、「立方体の各面に垂直な方向に正四角柱の穴をあけた立体をA、B、Cの3点を通る平面で切ったとき、切り口に現れる図形を描きなさい。ただし、各穴の正方形の一辺は立方体の一辺の1/3とする」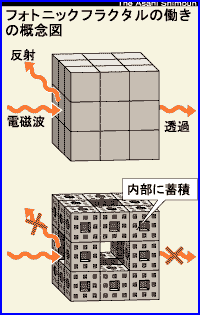 記事を要約すると、フラクタルな穴のあいた立方体に電磁波を投射すると、投射をやめたあとも電磁波が1000万分の1秒ほど、内部に留まるというもの。名づけて「フォトニックフラクタル」。これが、どんなにスゴイことかというと、朝日新聞の見出しにあるように、空中からエネルギーを採取できるということ。携帯電話の充電は必要なくなるし、光だって無数のフラクタルな穴に閉じ込め、必要なときに取り出すことができる(電気を蓄える「電池」ならぬ「光池」)。と、今世紀最大の発見と、朝日新聞の1面で大々的に紹介されたのだ。
記事を要約すると、フラクタルな穴のあいた立方体に電磁波を投射すると、投射をやめたあとも電磁波が1000万分の1秒ほど、内部に留まるというもの。名づけて「フォトニックフラクタル」。これが、どんなにスゴイことかというと、朝日新聞の見出しにあるように、空中からエネルギーを採取できるということ。携帯電話の充電は必要なくなるし、光だって無数のフラクタルな穴に閉じ込め、必要なときに取り出すことができる(電気を蓄える「電池」ならぬ「光池」)。と、今世紀最大の発見と、朝日新聞の1面で大々的に紹介されたのだ。 「フラクタル」といえば、「コッホ曲線」や「シルピンスキーのギャスケット」が有名だが、それを立方体にしたのが、「フォトニックフラクタル」だ。フラクタル図形は、細部を取り出したときにも全体の図形と相似しているのが特徴。究極の姿を考えると、2次元なのに面積がない、立方体なのに体積がないというようなおかしなことになる。次元数を考えると、とても中途半端な次元になる、不思議な図形なのだ。朝日新聞の記事を読んでも「フォトニックフラクタル」がどのように作用しているかは、依然不明でよくわからない。ひょとして、中途半端な次元に電磁波や光が吸い込まれちゃうのかぁ~と思いたくなる。
「フラクタル」といえば、「コッホ曲線」や「シルピンスキーのギャスケット」が有名だが、それを立方体にしたのが、「フォトニックフラクタル」だ。フラクタル図形は、細部を取り出したときにも全体の図形と相似しているのが特徴。究極の姿を考えると、2次元なのに面積がない、立方体なのに体積がないというようなおかしなことになる。次元数を考えると、とても中途半端な次元になる、不思議な図形なのだ。朝日新聞の記事を読んでも「フォトニックフラクタル」がどのように作用しているかは、依然不明でよくわからない。ひょとして、中途半端な次元に電磁波や光が吸い込まれちゃうのかぁ~と思いたくなる。
 まずは例題「図のような直角に曲がった幅1mの通路で運ぶことのできる長方形のソファーの最大面積を答えなさい」
まずは例題「図のような直角に曲がった幅1mの通路で運ぶことのできる長方形のソファーの最大面積を答えなさい」 これに対してコマ大数学研究会の面々は、「1平方メートルまではいきませんよね」と、竹内薫センセに助けを求めるが、「数学的には入るということで…」と薫センセも困惑ぎみだ。「引越し屋さん的には、そうはいきません」ダンカンの言うとおり、現実的には、1mの通路に1mの幅のソファーを通せと言われても、引越し屋としてはコマってしまうだろう。必ず「余裕」、「遊び」が必要だ。
これに対してコマ大数学研究会の面々は、「1平方メートルまではいきませんよね」と、竹内薫センセに助けを求めるが、「数学的には入るということで…」と薫センセも困惑ぎみだ。「引越し屋さん的には、そうはいきません」ダンカンの言うとおり、現実的には、1mの通路に1mの幅のソファーを通せと言われても、引越し屋としてはコマってしまうだろう。必ず「余裕」、「遊び」が必要だ。 それはともかく、長方形の場合も、面積は1平方メートルになるとのこと。
それはともかく、長方形の場合も、面積は1平方メートルになるとのこと。 東大生の解答は、円を半分にした形。面積は「Π/2」で約1.57平方メートル。マス北野は、角を曲がりやすくするため、ヘコみを入れると、さらに面積の大きなソファーを通すことができることまで気が付いたが、具体的な形、最大面積までは出すことができなかった。結論から言うと受話器のような「ハマースレー型」になるらしい。
東大生の解答は、円を半分にした形。面積は「Π/2」で約1.57平方メートル。マス北野は、角を曲がりやすくするため、ヘコみを入れると、さらに面積の大きなソファーを通すことができることまで気が付いたが、具体的な形、最大面積までは出すことができなかった。結論から言うと受話器のような「ハマースレー型」になるらしい。 数学的なことはともかく、このヘンテコな形をしたソファーが1m幅の直角の通路をすり抜ける様を見せられたら納得するしかない。さらに「ハマースレー型」の角を少し丸めた「ガーバー型」もあるらしい。
数学的なことはともかく、このヘンテコな形をしたソファーが1m幅の直角の通路をすり抜ける様を見せられたら納得するしかない。さらに「ハマースレー型」の角を少し丸めた「ガーバー型」もあるらしい。 通路の壁に沿って90度回転する「ハマースレー型」のソファーを見て、マス北野は「ロータリーエンジンみたいな動き」と称したが、興味のある人は、Wikipedia「
通路の壁に沿って90度回転する「ハマースレー型」のソファーを見て、マス北野は「ロータリーエンジンみたいな動き」と称したが、興味のある人は、Wikipedia「