少し、時間に余裕ができたので、前回の「たけしのコマネチ大学数学科」で出題された「ヨセフスの問題」を復習してみたいと思う。
問題「200枚のカードが1から順に並んでいます。1番上のカードを1番下に持っていき、次のカードを捨てるという作業を繰り返したとき、最後に残るカードは何番か答えなさい」
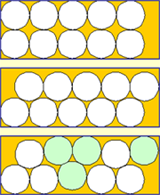
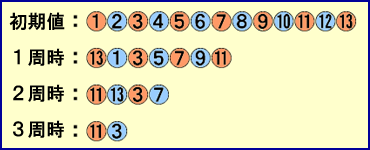 番組内では200枚のカードだったが、簡略化して13枚のカードで試してみよう。1枚おきにカードを捨てていくので、2周目に入るとき、奇数枚なので、数え始めた「1」のカード(トップ)は捨てられる。残りカードは7枚なので、3周目でもがトップが入れ替わる。残り枚数は4枚なので、トップの入れ替わりは起こらず、「11」枚目が最後に残るカードとなる。
番組内では200枚のカードだったが、簡略化して13枚のカードで試してみよう。1枚おきにカードを捨てていくので、2周目に入るとき、奇数枚なので、数え始めた「1」のカード(トップ)は捨てられる。残りカードは7枚なので、3周目でもがトップが入れ替わる。残り枚数は4枚なので、トップの入れ替わりは起こらず、「11」枚目が最後に残るカードとなる。
これを数式にすると、カードが偶数の場合は(2n)枚、奇数の場合は(2n+1)枚のカードがある。1周した時点で残るカードの枚数は、偶数の場合(2n/2^2)、奇数の場合は(2n/2^2)+1になる。3周時は(2n/2^3)……と続き、最終的に(2n/2^s+1)+1となるはずで、f(n)=2(n-2^s)+1という式になる。
ここでの「s」とは、何周したかであり、つまり2の何乗かであるかだ。
番組内でも、カードが200枚の場合、それを2進数で表し、「1」のところは「0」、「0」のところは「1」として、その数を引くと、最終的に残るカードを求めることができると解説していた。
で、いきなり説明もなく、結論だけを「nを2進数で表し、頭の1を取り、最後尾に付け加える」としたわけだが、これは、ビット演算という手法。10進数を「DEC2BIN」関数で2進数に変換し、先ほどの「2(n-2^s)+1」の式にあてはめてみる。
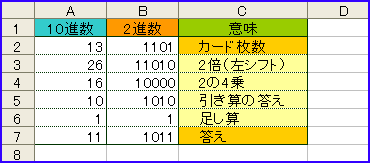 「2n」は、2進数の場合、左シフト、ローテーションを行うと、その数を2倍したことになる。たとえば、13の2進数である「1101」を左にひとつずらすと、「11010」になり、それを10進数で表すと「26」。それから「2(2^3)」を引くということは、「2^4」だから、二進数では「10000」、十進数では「16」を引いて、「1」を加えると、答えは、2進数表記で「1011」、十進数表記では「11」となるわけだ(コンピュータの内部では、こんなふうに2進数のビット演算で計算が行われているんですね)。
「2n」は、2進数の場合、左シフト、ローテーションを行うと、その数を2倍したことになる。たとえば、13の2進数である「1101」を左にひとつずらすと、「11010」になり、それを10進数で表すと「26」。それから「2(2^3)」を引くということは、「2^4」だから、二進数では「10000」、十進数では「16」を引いて、「1」を加えると、答えは、2進数表記で「1011」、十進数表記では「11」となるわけだ(コンピュータの内部では、こんなふうに2進数のビット演算で計算が行われているんですね)。
このブログは「たけしのコマネチ大学数学科」で出題された問題を「エクセル」で解くことを目的としているが、私を含め、数学にあまり縁のない人にも、とりあえず、難しく考えず「エクセル」を使えば、答えが出せるよ……というのが趣旨だったはず。
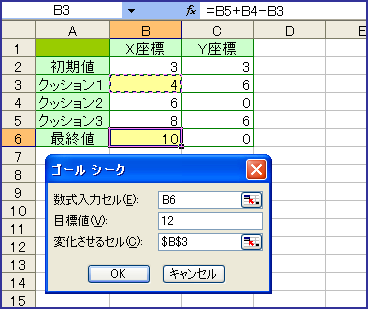
 ビット演算なんて、普通の生活の中では、使いません……というか「エクセル」では、10進数を2進数に変換することはできても、AND OR NOT などの論理演算子は、「真:TRUE」か「偽:FALSE」を返すだけで、ビット演算をすることができません。ましてや、左シフト命令なんてありません。そこで文字列操作で「=RIGHT(B2,LEN(B2)-1)&LEFT(B2,1)」とし、左の1文字を取って、右の末尾に加えています。
ビット演算なんて、普通の生活の中では、使いません……というか「エクセル」では、10進数を2進数に変換することはできても、AND OR NOT などの論理演算子は、「真:TRUE」か「偽:FALSE」を返すだけで、ビット演算をすることができません。ましてや、左シフト命令なんてありません。そこで文字列操作で「=RIGHT(B2,LEN(B2)-1)&LEFT(B2,1)」とし、左の1文字を取って、右の末尾に加えています。
今後は、わかりにくい「美しさ」よりも「たけし軍団:数学研究会」のメンバーになったつもりでがんばります。今回、唯一、正解を出したのは、じつは「数学研究会」ですもの。難しい理屈なんて、わからなくても、楽しければいいんだ……。