国際エミー賞の最終候補4作品に選ばれたけれど、残念ながら受賞を逃してしまった「たけしのコマネチ大学数学科」第69講。エミー賞の女神とは、赤い糸で結ばれてなかったのね。というわけで、今回は「運命の赤い糸」
問題:どこが交差しているかわからない、8本の赤い糸を男女8人がひとり2本ずつ選んで結ぶ。赤い糸が大きなひとつの輪になる確率を求めよ。
【遊び方】は続きを見てね。

What are you studying?
国際エミー賞の最終候補4作品に選ばれたけれど、残念ながら受賞を逃してしまった「たけしのコマネチ大学数学科」第69講。エミー賞の女神とは、赤い糸で結ばれてなかったのね。というわけで、今回は「運命の赤い糸」
問題:どこが交差しているかわからない、8本の赤い糸を男女8人がひとり2本ずつ選んで結ぶ。赤い糸が大きなひとつの輪になる確率を求めよ。
【遊び方】は続きを見てね。
以前のエントリで、木下眞二氏の考案した数学パズル「ゼロの誕生」を紹介した。そのとき、私のしたことは、4桁、5桁の整数の二乗をひとつひとつチェックして元の数と同じ桁数の「0」が含まれる数を抜き出したにすぎない(詳しくは過去記事を参照のこと)。木下眞二氏からは「数学文化(No.8 2007)」という本に「ゼロの誕生」の解説記事が掲載されていると教えていただいたものの、数学落ちこぼれの爺には、ちょっと難し過ぎる本というイメージが強く、敬遠していたんだよね。だいぶ日が経ってしまったけれど、アマゾンで取り寄せ、読んでみてた。
木曜深夜、フジテレビは「たけしのコマネチ大学数学科」の前に「もやしもん」というアニメを放映している(関東圏だけかも)。菌が肉眼で見えてしまうという特異能力を持つ青年が主人公で、これがおもしろい。で、「粘菌が迷路を解く」という話題をちらっと取り入れていた。実際に北海道大学で、その「粘菌」を見た、竹内薫センセの「コマネチ大学数学科」の第68講。今回は粘菌問題でも、年金問題でもなく、「時空図」ずら。
問題:A氏は外出先のB地点で、5時に迎えの車が来て帰る予定だった。ところが、用事が早く終わったので、B地点を4時5分に出発し、徒歩で家に向かい、途中で迎えの車に乗って帰った。この場合、B地点で5時まで車を待って帰るのと比べて何分早く家に着くか。A氏の歩く速さは時速4Km、車の速さは時速40kmとする。
人と車の速度を設定し、青い矢印をドラッグして出発時刻を設定してね(※註:秒単位は、数値を丸めず、切り捨てている)。
問題:互いに1メートルの距離をおいて3匹の猫がいる。この3匹の猫を結ぶ線の内側に1匹のノミがいる。ノミは、いずれかの猫めがけてジャンプするが、たえず目測を誤り、目標とする猫の半分の距離までしか跳べない。ノミは目標とする猫を気まぐれに選び、ジャンプを繰り返す。はたして、ノミは猫にたどりつくことができるか。また、ノミが着地できる場所はどの部分か。もしも、ノミが着地した場所に印をつけていくと、面積はどのくらいになるか。
ノミの軌跡がどんな図形になるかを思い浮かべて、画面内をクリックしてね。
道路公団が分割民営化されても、いっこうに高速道路の料金は下がらないし、ガソリン値は高騰。物流コストは経済、物価への影響大だ。郵政三事業が分割民営化されたが、手数料が下がるどころか、何倍にも跳ね上がった。いったい何のための分割民営化なのだ。この憤懣をどこにぶつけたらいいの「たけしのコマネチ大学数学科」第67講は「円分割」。
問題:円を20個以上に分割するには、最低何本の直線が必要か?
紙と鉛筆代わりのFlashを用意した。前エントリで線分の交差判定をズルしたが、いきなり、その線分交差判定が必要になった。いちおう、トライしてみたのだが、どうも、うまくいかない。理解するには、時間がかかりそうなので、とりあえず、分割数は自分で数えてね><;
追記(11月10日):分割数を表示した^^;
前回の「コマネチ大学数学科66講:ピックの定理」の復習。格子点を繋いで描いた多角形の面積は、ピックの定理によって「面積(S)=内包点(I)+境界点(B)÷2-1」と表すことができる。いろいろな多角形を描き、ピックの定理で面積を計算するFlashムービーを作成した。
格子点をクリックして多角形を描く。終点を始点に結ぶと多角形の内部が塗りつぶされるので「計算」ボタンを押してほしい。
「ピック?子豚さん? 私も太り過ぎないように頑張ります。ブヒッ、ブヒー!」というオープニングの戸部アナに「それは、ピッグだろ」と、ひとり、むなしくテレビ画面にツッコミをいれつつ「たけしのコマネチ大学数学科」第66講。始まり、始まりー。
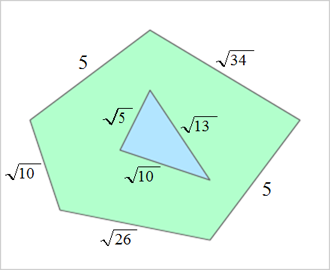
問題:碁盤の目のように等間隔に道が通っている図のような形の街がある。この街の中には交差点が37個ある(外周上にある5つの交差点は含まない。街の中央にある池の中の交差点(?)は含む)。外周の長さ、池の周囲の長さは図の通り。この街の面積(陸地のみ)を求めよ。