コイズミが一言「鈍感力が大事だ」といえば、渡辺淳一の「鈍感力」が売れる今日この頃、私は「老人力」でがんばるの「たけしのコマネチ大学数学科」第39講。お題は「モンモール問題」。
問題:6人でプレゼント交換するとき、自分のプレゼントをもらわない組み合わせは何通りか。
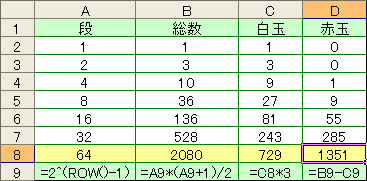
まず、少ない人数で考えてみる。2人のときは、お互いプレゼントを交換するだけなので1通り。3人のときは、2通りしかないことがすぐにわかる。4人の場合、A,B,C,Dとすると、Aは、B,C,Dとプレゼント交換する組み合わせが考えられ、残り3人は2通りと、2人の1通りの組み合わせになり、3*(2+1)で9通りになる。ここから漸化式を導くと、f(n)=(n-1)*((f(n-1)+f(n-2))となる。
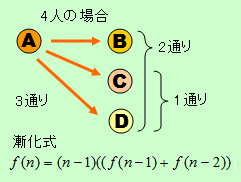
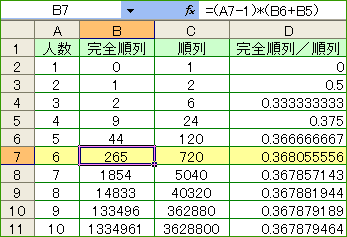
この漸化式をもとに「エクセル」で表を作成した。というわけで、6人の場合は、265通りという答えが得られた。
中村亨センセの「美しき数学の時間」で解説されていたように、この漸化式を一般化すると(一般項nをどんどん増やしていくと)、
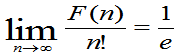
となるらしい。出ました、自然対数の底、ネイピア数が^^;

「エクセル」では、自然対数の底は「=EXP(1)」で求めることができる。つまり、1/eは、「=EXP(-1)」だ。人数がたった6人でも、かなり、この値に収束してきているのがわかる。
前回の予告で「次回は有名人の誕生日パーティ?」とあったので、すっかり、今回は、誕生日が一致する確率の問題かな……とヤマをかけたが、2月25日は、戸部アナの26歳の誕生日だそうで、コマ大数学研究会が扮する、戸部洋子だらけの誕生日パーティーだった^^;
「メガネの洋子、千葉県検見川~♪」というわけで、お誕生日おめでとうございます。「似てないですよ~」と文句を言われそうだけど……^^;