コイズミが一言「鈍感力が大事だ」といえば、渡辺淳一の「鈍感力」が売れる今日この頃、私は「老人力」でがんばるの「たけしのコマネチ大学数学科」第39講。お題は「モンモール問題」。
問題:6人でプレゼント交換するとき、自分のプレゼントをもらわない組み合わせは何通りか。
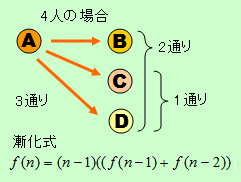
まず、少ない人数で考えてみる。2人のときは、お互いプレゼントを交換するだけなので1通り。3人のときは、2通りしかないことがすぐにわかる。4人の場合、A,B,C,Dとすると、Aは、B,C,Dとプレゼント交換する組み合わせが考えられ、残り3人は2通りと、2人の1通りの組み合わせになり、3*(2+1)で9通りになる。ここから漸化式を導くと、f(n)=(n-1)*((f(n-1)+f(n-2))となる。
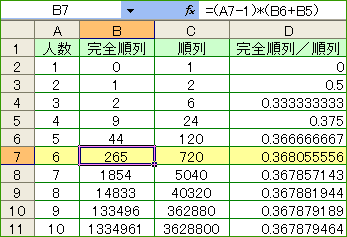
この漸化式をもとに「エクセル」で表を作成した。というわけで、6人の場合は、265通りという答えが得られた。
中村亨センセの「美しき数学の時間」で解説されていたように、この漸化式を一般化すると(一般項nをどんどん増やしていくと)、
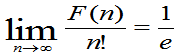
となるらしい。出ました、自然対数の底、ネイピア数が^^;

「エクセル」では、自然対数の底は「=EXP(1)」で求めることができる。つまり、1/eは、「=EXP(-1)」だ。人数がたった6人でも、かなり、この値に収束してきているのがわかる。
前回の予告で「次回は有名人の誕生日パーティ?」とあったので、すっかり、今回は、誕生日が一致する確率の問題かな……とヤマをかけたが、2月25日は、戸部アナの26歳の誕生日だそうで、コマ大数学研究会が扮する、戸部洋子だらけの誕生日パーティーだった^^;
「メガネの洋子、千葉県検見川~♪」というわけで、お誕生日おめでとうございます。「似てないですよ~」と文句を言われそうだけど……^^;


コマネチ大学 #39
たけしのコマネチ大学#39
2007/02/22 深夜OA
今回のテーマは、
「モンモール問題」
◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇
1708年にフランスのモンモール氏がトランプ13枚を用いた問題に由来し、
あのオイラーが研究したことでも有…
今晩は。
OnAirでは、1/eになる過程にもう少し突っ込んで欲しかったところです。それにしても挿絵が見事ですね。私の記事にも紹介してしまいました。
では、失礼いたします。
I appreciate in your usual cooperation.
Best Regards,Chablis
漸化式を作るまでの過程がわかりにくかったので、考えてみました。
A、B、C、Dの持っていたプレゼントをa、b、c、dとする。
Aはb、c、dのいずれかをもらうので3通り考えられる。
Aがbをもらったとき、
(1)Bがaをもらったとき、C、Dの2人はc、dの交換をするときだから1通り。
(2)BがaをもらわないときはB、C、Dの3人がb、c、dの交換をするときと同じだと考えられるので3通り。(aはbと同じ扱いになる)
(1)(2)よりAがbをもらったときは3通り。
すみません。
(2)は3通りではなく、2通りの間違いです。
原さん、コメントありがとうございます。
恥ずかしい話ですが、懺悔します。爺は初めて「漸化式」という言葉を見たとき、なんとなく、ルパン三世に登場する、石川五ヱ門の「斬鉄剣」のイメージが湧いて、「ざんかしき」と読んでしまったのでした><;
で、「漸化式(ぜんかしき)」の意味も、一般式を導くための暫定的な式だろうと……。こーなると、読みまつがいによる思い込みも甚だしく、恥ずかしいというより、冷や汗もの。もちろん、漸化式とは、a(n)=a(n-1)*b のように、数列 a(n)の値が順々に定まっていくような式のことです。
「数学」を基礎から学んでないから、こんな間違いをするんですね。幸い、爺の場合、誰かに「この、ざんかしきは…」などと言う前に気がついたからよかったけれど、麻生太郎首相の場合は、「頻繁」を「はんざつ」、「踏襲」を「ふしゅう」、「未曽有」を「みぞゆう」などと読み間違え、それが全国にテレビ放映されちゃったから、恥ずかしいどころの話じゃないですよね。「はんざつ(煩雑)に行き来して交流している」って、なんか、すげー迷惑しているって感じで、相手の国に失礼でしょ^^; 麻生さんは、「国語」を基礎から学んでほしい。(爺が言うな^^;)
どうもこんばんわ。
実は、12人くらいのプレゼント交換で全員他人のプレゼントに当たったことがあります。
これは奇跡なのではないか?と思ったので、確率をエクセルで計算すると1/eに収束したので驚いた記憶が。直感的には0に収束しそうなんですけどね。
プレゼント交換に参加した人全員にこの結果を展開しても、誰一人反応してくれなかったのが物凄く悲しかったですが。。。
で、以前は1/eに収束する証明までできなかったので、今回この証明をして見ました。
n人のプレゼント交換で全員他人のプレゼントに当たる場合の数(モンモール数)を
a(n)とおく。
a(n) = (n-1)(a(n-1) + a(n-2))
確率はこれをn!で割れば良いから、
b(n) = a(n) / n!
とおける。a(n)の漸化式からb(n)の漸化式が求められ、
n b(n) = (n-1) b(n-1) + b(n-2)
両辺からn b(n-1)を引いて、
n (b(n)-b(n-1)) = -(b(n-1)-b(n-2))
b(n)-b(n-1) = (b(n-1)-b(n-2))/(-n)
これより、帰納的に
b(n) – b(n-1) = (-1)^n / n!
b(n) = Σ(-1)^n / n!
右辺はexp(x)のテーラー展開だから、
n→∞ b(n)→exp(-1)=1/e