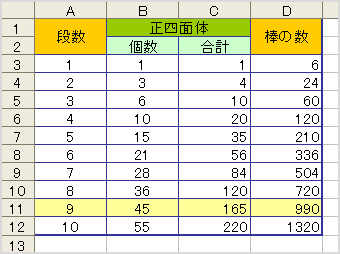
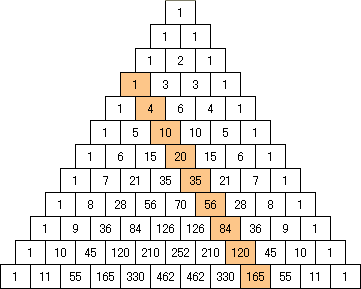
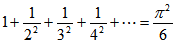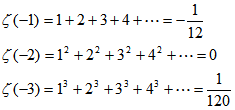先日、NHKスペシャル「Google革命の衝撃」が放送された。その中で、Googleの人材募集の広告が紹介されていた。人材募集なのに「Google」の文字は、どこにもなく、「{eの値で、最初に出てくる10桁の素数}.com」とあるだけの広告だ。
ネットで調べてみると、これは、数年前の出来事らしい。そういえば、そんなことがあったかも知れないと、かすかに記憶が甦ってきたが、たぶん、当時は「へえぇ」という感じでスルーしていたのだろう。
で、「コマネチ大学数学科」が始まるまでの間、この問題をあらためて考えてみた。自然対数の底「e」の値といったら「ネイピア数」だ。
■たけしの誰でもピカソ:ネイピア数e相性診断
2億桁のネイピア数の中から、ふたりの誕生日が何桁目に登場するかを調べてくれる。しかし、自分の誕生日4桁と相手の誕生日4桁で、8桁にしかならない。しかも、月は12、日は31までと、入力できない数が多すぎる。これでは役に立たない;;
しょうがないので、「エクセル」で作ろうと思ったが、エクセルのMOD関数は、10桁の数値には対応していない;; VBAを使えば、なんとかなりそうな気がするが、なんか面倒なことになりそうで気後れする。手軽に出来るのは、FlashのActionScriptだ。ネイピア数は、ひとまず置いといて、問題を簡単にするため、適当な文字列「222215722222」の先頭から順に3文字ずつ抜き取って、それが素数であるかどうかをチェックする、FlashのAction Scriptを書いてみる。
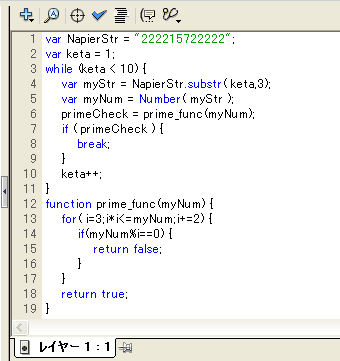
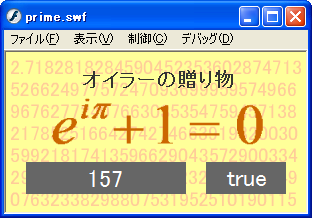
動作チェックをすると、確かに「222215722222」の文字列から「157」を抜き出し、それが「素数」であることを判断している。白状すると、素数かどうかのチェックは「Wikipedia」の「素数判定」の項目から、引用させてもらった。
ここまでくれば、あとは簡単。最初の文字列に「自然対数の底e」の値(ネイピア数)を入れ、抜き出す文字列の数を「10」にするだけだ。
自然対数の底「e」の値は、以下のサイトでも入手可能……。
■eの値
しかし、500億桁もいらないんですけど^^; 最初の1億桁だけでも、55MBもある。解凍すると、117MBのテキストファイル;;「エクセル」では、全部を読み込めなかった。
■自然対数の底
こちらは、指定した桁数の「自然対数の底」の値を表示することができるので、便利だ。とりあえず、250桁を表示してコピーし、それを、FlashのActionScriptに貼り付ける。
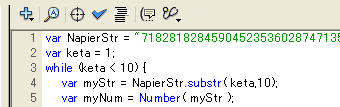

「なぬ~っ!」動作チェックでは、うまく動いてくれたのに、「False」だとぉ~;; あれこれ悩んでみたが、うまい解決策が思いつかない。たぶん、どこかでオーバーフローしているのだろう。いつも「結果が出ればいいや」と、コマ大数学研究会ばりの体当たりプログラミングをしているから、こういうことになる。やはり、基礎ができてないと、こういうところでボロが出る。付け焼刃の数学の知識ではダメらしい。「アホなことやっているなぁ」と思った方は、迷える酔っ払いの爺に愛の手を!
(1月26日追記:ループ数が10のままだぁ^^;;)
(1月27日追記:偶数を除外していなかった;;やっと正解に!)
数年前の問題なので、ネットで調べれば、正解はわかる。正解は「7427466391」。
2.718281828459045235360287471352662497757247093699959
5749669676277240766303535475945713821785251664274274
6639193200305992181741359662904357290033429526059563
0738132328627943490763233829880753195251019011573834
で「7427466391.com」へアクセスすると、次の問題が提示される。
《以下、引用》
Congratulations. You’ve made it to level 2.
Go to www.Linux.org and enter Bobsyouruncle as the login
and the answer to this equation as the password.
f(1)= 7182818284
f(2)= 8182845904
f(3)= 8747135266
f(4)= 7427466391
f(5)= __________
《引用終わり》
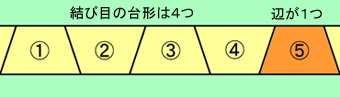
こちらの問題は、f(1)~f(4)の数値が10桁で、すべての数値を足すと「49」になることに気が付けば、さほど、難しくはない。これなら「エクセル」でも、解けるぞ。
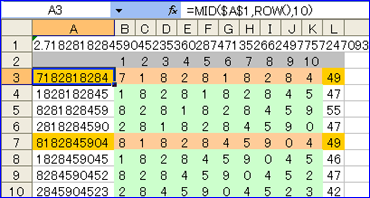
セルA1に、先ほどの「自然数の底」サイトからコピーした数値を貼り付ける(セルの書式設定は文字列にしておく)。MID関数を使って、1文字ずつ、移動させながら10文字分を抜き出す。オートフィルの連続入力をするため、行番号を求める、ROW関数を使って、抜き出す文字列の開始位置を求めている。さらに、抜き出した文字列を1文字ずつ分解して数値に換え、「=VALUE(MID(A3,$B$2,1))」その合計を出す。合計が「49」になる行を見ると、f(1)~f(4)の値になることを確認できる。

5番目の数値は、129行目に出現する。ネイピア数の小数点以下、127桁目だ。
結局、「コマネチ大学数学科」が始まるまでの小手調べのつもりだったが、番組が始まっても、こちらの問題に気をとられたまま、酔いが限界に達している。なんとしても、この記事をアップしてから、眠りにつこう。今回の「コマネチ大学数学科」の問題は、かなり難しいという印象……。
今回、参考にした素数についてのサイト
■a prime number
1から2147483647までの素数を計算する。残念;;10桁だが、「9999999999」まで表示できないと、今回の問題には対応できない;;
■ゆいのホームページ:ソフトウェア&小技メモ
341,550,071,728,321以下の素数(15桁)を、1個当り数秒で求める。短時間で素数を判定するアルゴリズムのキーワードは「2,7,61」? このサイトを利用すれば、10桁の素数表を作成することができるが、素数表とネイピア数とのマッチングを試みる方法は、いささか、現実的でないような気がする。
■AjaxによるRSAアルゴリズム体験
360桁の素数でも一瞬で表示する。なんで、こんなに速く素数を生成できるの? 素数生成のアルゴリズムは、いくつかあって、それが素数であるかどうかを検証することのほうが難しいのか……。いわゆる、因数分解するほうが大変という「N≠NP」問題なのかな?