部屋の電灯つけっ放し、テレビつけっ放しで、酔いつぶれて寝ていたが、番組が始まると、ハッと目が覚めた「コマネチ大学数学科」の第34講。もちろん、前回の轍を踏まじと、しっかり録画予約してあったのだが、朦朧とした頭で番組を見終わると、再び夢の中へ……。夢の中では、なにやら難しい数式が出てきて「わかったぞ!」と叫んでいたが、それがなんであったか覚えていない。
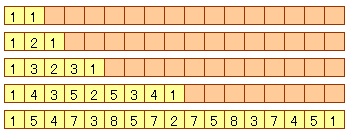
問題は、隣り合う数の和を下図のように加えていく作業を1万回繰り返し行ったとき「101」という数は、何回出現するでしょうか。
番組では触れられていなかったが、これは「チューリング・マシン」ではないかと思う。チューリング・マシンとは、コンピュータが登場する以前の1937年、アラン・チューリングが発表した「計算可能な数-決定問題に対する応用」という論文に登場する仮想的な装置のこと。
チューリング・マシンは、マス目が書かれた長~~い紙テープと、ひとマスごとに移動できるヘッドから出来ている。ヘッドはマス目に書かれている記号を読み込んだり、書き込んだり、消去することができると想定されていた。なにせ、仮想の装置なので現実にそういう装置があったわけではない。
アラン・チューリングは、こんな簡単な仕組みの装置でも、命令次第でさまざまな演算ができることを証明して見せたんだよね。これがコンピュータの登場につながった。昔の映画などに登場するコンピュータはオープンリールのテープ(外部記憶装置)がガチャガチャと動いている映像があるでしょ、そんなカンジ。
チューリング・マシンのヘッドは、マス目の数字を読み込んで、足し、書き加えていく。テープを巻き戻して、最初からもう一度……さて、この作業を1万回繰り返すと「101」という数は何回出現するか……という問題に置き換えられる。
コマ大数学研究会は、手作業でテープに数字を書き、足していった。最初の「1、1」と書かれたテープを1本目とすると、14本目で「40」個という答えを出した。このときのテープの長さをチューリング・マシンのマス目の数で表すと「2^(14-1)+1」で、8193となる。8193個のマス目の中に「101」は40回出現したというわけだ(コマ大数学研究会が計算ミスをしていないと仮定しての話^^;検証はしていない;;)。
無理やり、ひとつのマス目をコンピュータのメモリ(1バイト)に対応させてみると、8193バイト、約8キロバイト。日本で組み立てキットの「マイコン」が登場したときは、確かメモリが8キロバイト程度だった。しかし、この計算を1万回ではなく、100回繰り返したとしよう。そのとき必要なメモリはどのくらいになるというと……。
「2^(100-1)+1」で「6.33825E+29」。これをテラバイト(10^12=1兆バイト)で割ると、63京テラバイトにもなってしまう。1万回なんて、とんでもない。どれだけ長いテープを用意しなきゃならないの! 体当たりのコマ大数学研究会にとっては、酷過ぎる;;。
で、マス北野は、今回も冴えていた。3、5、7などの素数の出現数は「n-1」になっていることを発見。答えは「101-1」で「100」。東大生コンビは時間切れで、マス北野、ただひとりが正解した。
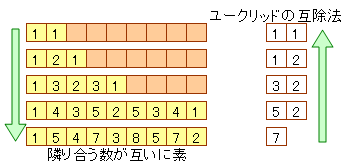
竹内薫センセの「美しき数学」の時間では、この問題の解法を「ユークリッドの互除法」(参照:~さんすう・数学のお勉強~)を使って解説。素数を「n=a+b」のように表すと、必ず、aとbは互いに素(最大公約数が「1」)になるという。通常の約分法ではないが、例えば「7」を「5+2」のように分けて、小さいほうの数を残し、大きい数から小さい数を引くと「3,2」のようになり、最終的に「1,1」となる。これはちょうど、問題を逆のぼる形になる。「7」を「a+b」のような形にできる組み合わせは「6,1」「5,2」「4,3」「3,4」「2,5」「1,6」の6通り。つまり「101」の場合は、「101-1」で「100」個ということになるらしい。
番組の冒頭で、980万桁の素数を紹介していたが、竹内薫センセ曰く「素数は大きな広がりを持っている。宇宙が素粒子で出来ているように、数学では、素数が重要な存在」と。番組では、素数を「素敵な数」と表現していた。数学に素養のない私は、素敵な人ではなく、ただの「素人」(シロウト)だ^^;
竹内センセの「薫日記」の1月17日のエントリ「重版おめでとう!」で中村亨センセの「数学21世紀の7大難問」の重版が決定したことを知り、これを機会に「薫日記」から注文した。まだ届いていないのだけれども、私もアフィリエイトをば……。
 数学21世紀の7大難問 著者:中村 亨 |

>コマ大数学研究会は、手作業でテープに数字を書き、足していった。最初の「1、1」と書かれたテープを1本目とすると、14本目で「40」個という答えを出した。このときのテープの長さをチューリング・マシンのマス目の数で表すと「2^(14-1)+1」で、8193となる。8193個のマス目の中に「101」は40回出現したというわけだ(コマ大数学研究会が計算ミスをしていないと仮定しての話^^;検証はしていない;;)。
計算してみると14本目では「101」は52回出現するはずだと思います。
初めに出現するのは11本目に8個でした。
例:101=8+93=8+(11×8+5) より
(8,5)→(8,13)→(8,21)→・・・→(8,93)→「101」
(8,5)は5本目に出てくるので(8,93)は11+5=16本目
故に「101」は17本目に出現します。
(1,100)~(50,51)まですべて計算して何本目に何個出現するかまとめました。
(もちろん2倍済み,ただし以前に出現した「101」は個数に含まない)
11本目→8個
12本目→8個
13本目→16個
14本目→20個 ここまでの総計52回出現
15本目→4個
16本目→4個
17本目→8個
19本目→4個
20本目→2個
21本目→4個
22本目→4個
25本目→4個
29本目→4個
36本目→4個
52本目→4個
101本目→2個
(その他→0個)
合計100個
ひたすら場合分けしていったやり方ですので、何か14本目までの総計を出す良い方法があれば考えてもらえないでしょうか?
問題で「1万回繰り返す」としたのは十分大きいところでは出現することは無いことを言いたかったと思われます。実際、素数nが最後に出現するのはn本目の「1+(n-1)」と「(n-1)+1」の2個であると予想できます。
素数で無い数の場合は互いに素である数の和で表すことができる通りだけ出現すると予想できます。
例:4=1+3 ○
=2+2 ×
=3+2 ○
故に 「4」は2回出現
コマネチ大学 #34
たけしのコマネチ大学#34 2007/01/18 深夜OA
今回のテーマは、
「素数」
◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇
素数とは、1とその数以外では割り切れない数字のことです。
世界的な素数研究プロジェクトもあり、その調査によると、
2…
コメントの公開が遅れて、ごめんなさい。
チェックを怠っていました;;