わかっているようで、詳しくわかっていなかった「オーバーハング」問題(中村亨センセ談)の「たけしのコマ大数学科」。はたして「オーバーハング」を制して頂上に立つのは誰か?(戸部アナ談)
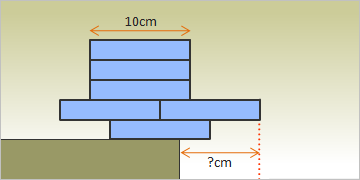
問題:幅、長さ、厚さ、重さがすべて同じな6枚の積木を積み重ね、台の端からせり出す長さが、できるだけ長くなるような積み方を答えなさい(※積木は水平に積むこと、斜めに立て掛けてはダメよ)。

What are you studying?
わかっているようで、詳しくわかっていなかった「オーバーハング」問題(中村亨センセ談)の「たけしのコマ大数学科」。はたして「オーバーハング」を制して頂上に立つのは誰か?(戸部アナ談)

問題:幅、長さ、厚さ、重さがすべて同じな6枚の積木を積み重ね、台の端からせり出す長さが、できるだけ長くなるような積み方を答えなさい(※積木は水平に積むこと、斜めに立て掛けてはダメよ)。
数学とマジックは似ている。結果だけを見ると、どうして、こんな答えにたどりつくのか、不思議なことがあるけれど、解法(種明かし)がわかってしまえば、納得する。でも、その種明かしがわからないと、まるで数学はマジックのようなんだよね「たけしのコマ大数学科」。
問題:ゲストが選んだ3桁の数「abc」の各桁の数を並び替えた5つの数、(acb)(bac)(bca)(cab)(cba)を足し合わせた数をマジシャンに伝えると、マジシャンは、元の数「abc」を当てる。では、5つの数の和が「3194」のとき、元の数「abc」はいくつか?
つまり「この数理マジックの種明かしをせよ」という問題。三桁の数「abc」を選ぶと、並び替えた5つの数の合計を表示。(↑)ボタンを押すと、マジシャン(?)が答える。
民主党の「はだかの王様」小沢代表の第一秘書が、政治献金規制法違反の疑いで逮捕された。自民党もパーティー券というかたちで、西松建設から資金を得ていた議員がぞろぞろ。「いいかげんに城」とゆーわけで、「たけしのコマ大数学科」。今回は、ヘンリー・アーネスト・デュードニー(1853~1930年)が考えたパズル「王様と城」の問題。
問題:城10個を城壁5列にそれぞれ4個ずつ並べる。城壁を越えなければ外から近づけない城が1個以上あるような、城の配置を考えなさい!
ルールを整理しておくと、城壁は直線。それぞれの城壁には城を4個配置すること。城の数は合計10個。問題図は、どの城も城壁を超えることなく、外から近づくことができるのでダメ。「Clear」ボタンを押し、マウスのドラッグ&ドロップで城壁(直線)を引いてほしい。図が完成したら、自分で城を置いて、全部で10個になるか、どうか確かめてね。
今回は、しょーもない爺の「話の枕」は、なしで、いきなり「たけしのコマ大数学科」。「アインシュタイン」が考えたとゆー問題のアレンジバージョン。なにせ、今回は、書くべき条件が多いのだ^^; 異なる色の5軒の家が並んでいて、そこには、異なる国籍の人が、異なる髪型で、異なる飲み物を飲み、異なるペットを飼っているという。さて、そこで、問題。
問題:魚を飼っているのは、どの国の人か?
1:イギリス人は赤色の家に住む
2:スウェーデン人は犬を飼う
3:デンマーク人は日本茶を飲む
4:緑色の家は白色の家の左
5:緑色の家の人はコーヒーを飲む
6:髪型が坊ちゃん刈りの人は鳥を飼う
7:黄色の家の人はリーゼント
8:中心の家の人は牛乳を飲む
9:ノルウェー人は一番目(左端)の家に住む
10:金髪の人は猫を飼っている人の隣に住む
11:馬を飼っている人はリーゼントの人の隣に住む
12:パンチパーマの人はビールを飲む
13:ドイツ人はスキンヘッド
14:ノルウェー人は青色の家の隣に住む
15:金髪の人の家は水を飲んでいる人の隣
【遊び方】条件をよく読み、条件に合う項目を「▲」、「▼」のボタンを押して選び、項目をマウスでドラッグ&ドロップして、表を完成させてほしい。表が完成すれば、おのずと、答えは明らかになる。
先日、テレビで一粒5万円のイチゴが紹介されていた。たしかに普通のイチゴと比べると、やたらデカイし、甘味もあるらしいのだが、いったい、どんな人が買うんだよ。爺は「いちご」より「いいちこ」のほうがいい「たけしのコマ大数学科」
≪ルールの説明≫
魔法A:その場にあるイチゴ、1個につき、イチゴとバナナに変える。つまり、イチゴの数はそのままで、イチゴの数だけバナナが増える。
魔法B:その場にあるバナナ、1本につき、バナナとイチゴに変える。バナナの数は変わらず、バナナの数だけイチゴが増える。
問題:「魔法A」と「魔法B」を使い、1個ずつあるイチゴとバナナを、イチゴ15個、バナナ877本にするには、魔法を合計、何回使えばいいか?
世の中は「バンアレン帯」ではなく、「バレンタイン」デー。人生いろいろ「たけしのコマ大数学科」。今回は、ビター島倉チヨコではなく、ピタゴラス。
問題:「3:4:5」の直角三角形の各辺を一辺とする、正三角形A、B、Cがある。AとBをふたつずつに切って、その断片を組み合わせて、正三角形Cを作れ!(※追記:断片を裏返ししちゃダメよ)
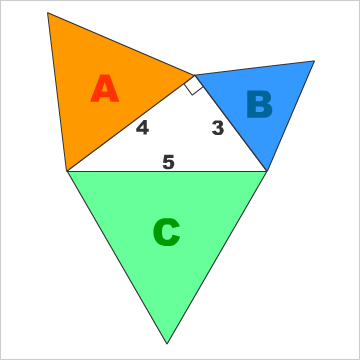
「ピタゴラスの定理」は有名だけれども「a^2+b^2=c^2」は、直角三角形の各辺に正方形を描いて説明される。でも、面積比なので、正方形でなく、正三角形でも、「a(√3/4)+b(√3/4)=c(√3/4)」になるわけね。
国民の信を問うことなく、安倍、福田、麻生と続いてきた内閣。「100年に一度の世界金融不安の時代」などと言っておきながら、だらだらと解散もできずにいる。小泉内閣の総務大臣だった麻生太郎が「郵政民営化には反対だった」などと国会で発言して、与党内も騒然だが、そう、今回は「内閣の和」ではなく、「内角の和」の「たけしのコマ大数学科」
問題:円周上に1~35まで点を打つ。1から7個ずつ飛ばして、点を線分で結び、星型の多角形を作るとき、その内角の和を求めよ。
多角形の内角の和といっても、円周上に接する頂点が作る角度の和だよ。
私大の受験シーズンということだが、マス北野は「5校受ける」と言って、親から受験料をもらい、明治大学だけ受験して、残りの受験料で遊びに行ったという「たけしのコマ大数学科」
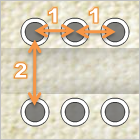
問題:1列に8個ずつ、計16個の穴があいた靴に、きちんと履けるように靴ひもを通したとき、最短の長さ(結び目までの長さ)を求めよ! それぞれの穴は、必ず、反対側の列の穴につながっていなければならない。穴どうしの距離は右図のとおり。
【遊び方】1度目にクリックした穴から、2度目にクリックした穴に「ひも」を通す。それの繰り返し。エラーチェックはしていないので、ちゃんと1本の「ひも」で結べるようにしてね。はたして、最短の結び方とは……?
マス北野の誕生日は、1947年1月18日(62歳)、木村美紀の誕生日は、1985年1月19日(24歳)、そして、中村亨センセの誕生日が1963年1月22日(46歳)と、誕生日ラッシュの「たけしのコマ大数学科」。確かにガダルカナル・タカが1956年12月16日生まれの52歳であることを考えると、中村亨センセ、かなり、老けて見えるような……。
問題:図のような十畳の日本間に畳を敷き詰める組み合わせは何通りあるか?
【遊び方】マウスのドラッグ&ドロップで畳を敷いてほしい。エラーチェックはしていないので、畳はどこにでも置けてしまうのと、一度、置いた畳は移動できないので注意してほしい。