
■コマネチ大学2006年度講義リスト


What are you studying?

竹内薫センセによると、3月で終了とのことだが、番組の最後に「1年間ありがとうございました」に続いて「4月からもマスマス数学します」というテロップが映った。どういうことなの?「たけしのコマネチ大学数学科」第42講。演題は「ガウス平面」。
問題:草原に1本のカシと1本のマツと1軒の小屋があります。小屋からカシまで歩き、右へ直角に同じ距離を歩いて、そこに棒を立てます。同様に小屋からマツまで歩き、左へ直角に同じ距離を歩いて、そこに棒を立てるとき、棒と棒の中間に宝があります。
宝がどの場所にあるか作図しなさい。ただし、小屋の位置はわかっていません。
「コマネチ大学数学科」第41講の「テトリスに挑戦」の類題を考えた。ルールは同じ。できるだけ凸型のブロックを使わないようにして、マス目を埋めること。下の問題をクリックすると、別窓で開くはず。(IE6のXPSP2とFirefox2.0.0.3でしか動作確認してない;;)マス北野のように2分で解けるかな^^;
またまた、「コマネチ大学数学科」38講の「スパゲッティ問題」である。茹でる前のスパゲッティを折る話なので、こんがらがることはないと思うのだが、私の頭の中では、複雑にからみついて、なかなか解きほぐせない。
前回の「スパゲッティ問題(その2)」では、モンテカルロ法でこの問題を解こうとしたら、期待したとおりの値にならなかった。変数名や図がひとりよがりでわかりにくく誤解を与えた部分があったので、そのへんを整理してみた。
今回は「テトリスに挑戦」ということで、マス目を3つの形のブロックで埋める問題なのだが、番組を見ている私たちは、ただ見ているだけでトライしてみることができない。そこで、マス目とブロックを用意しようとしたのだが、これがホントに大変だったのよ「たけしのコマネチ大学数学科」第41講。
問題:図の白いマス目を3種類のブロック全部を使って埋めるとき、凸型は、最低何個必要か?(できるだけ凸型を使わないで完成させよ!ということ)
コマネチ大学数学科38講の「スパゲッティ問題」で、大ポカをやらかした酔っ払い爺の私。コマ大数学研究会と同じく、モンテカルロ法で確認してみようと思った。
問題:1本が30cmのスパゲッティを無作為に3本に折ったとき、その3本で三角形を作ることができる確率は?
イタリアのちょい悪オヤジ風、竹内薫センセが和服を着て登場。マス北野の「崔洋一みてえだな」の一言に激しく同意「たけしのコマネチ大学数学科」第40講。お題は「和算」。以前、「百五減算」をやったが、今回は、なにやら幾何の問題。
今有如図直内容等円二ケ設二斜相錯載側円
其短径及等円径若干問得側円長径如何
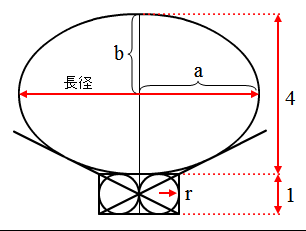
問題:この楕円の短径が4、等円の直径が1のとき、
楕円の長径を求めなさい。
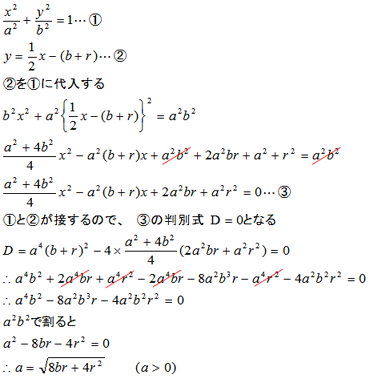
この式にb=2,r=1/2を代入すると、a=√9で「3」、長径はその2倍で「6」になる。
ならば、はじめから式を2倍にしてみる。

これが、算額の公式
置短径倍之加等円径乗等円径開平方二之得長径合問
というわけで、じつは、上で紹介した式は、ほとんど、以下のサイトから、書き写しただけ><;
一関市博物館:和算に挑戦
「美しき数学の時間」で紹介されていた解法、アファイン変換による解答例も載っている。なんだか、難しそうだったので、パス;;
また、「算法助術」(長谷川弘閲/山本賀前 編)は、電子復刻版が公開されている。二十八(82:右から読んでね^^;)にあるよ。
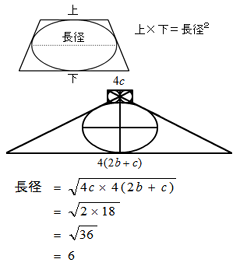
元の図形をひっくり返している。それにしても「和算」は、なかなか風情があってよろしいなぁ……。
コイズミが一言「鈍感力が大事だ」といえば、渡辺淳一の「鈍感力」が売れる今日この頃、私は「老人力」でがんばるの「たけしのコマネチ大学数学科」第39講。お題は「モンモール問題」。
問題:6人でプレゼント交換するとき、自分のプレゼントをもらわない組み合わせは何通りか。
まず、少ない人数で考えてみる。2人のときは、お互いプレゼントを交換するだけなので1通り。3人のときは、2通りしかないことがすぐにわかる。4人の場合、A,B,C,Dとすると、Aは、B,C,Dとプレゼント交換する組み合わせが考えられ、残り3人は2通りと、2人の1通りの組み合わせになり、3*(2+1)で9通りになる。ここから漸化式を導くと、f(n)=(n-1)*((f(n-1)+f(n-2))となる。
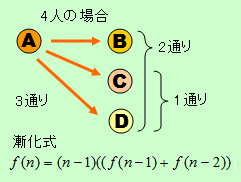
この漸化式をもとに「エクセル」で表を作成した。というわけで、6人の場合は、265通りという答えが得られた。
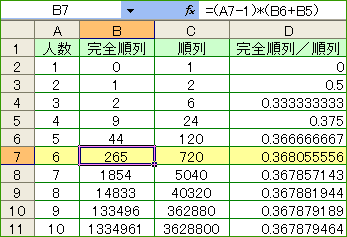
中村亨センセの「美しき数学の時間」で解説されていたように、この漸化式を一般化すると(一般項nをどんどん増やしていくと)、
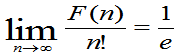
となるらしい。出ました、自然対数の底、ネイピア数が^^;

「エクセル」では、自然対数の底は「=EXP(1)」で求めることができる。つまり、1/eは、「=EXP(-1)」だ。人数がたった6人でも、かなり、この値に収束してきているのがわかる。
前回の予告で「次回は有名人の誕生日パーティ?」とあったので、すっかり、今回は、誕生日が一致する確率の問題かな……とヤマをかけたが、2月25日は、戸部アナの26歳の誕生日だそうで、コマ大数学研究会が扮する、戸部洋子だらけの誕生日パーティーだった^^;
「メガネの洋子、千葉県検見川~♪」というわけで、お誕生日おめでとうございます。「似てないですよ~」と文句を言われそうだけど……^^;

数ヶ月ぶりに電車に乗り、編集部での打ち合わせに出かけた、ひきこもり爺の「コマネチ大学数学科」受講メモ。
問題:1本が30cmのスパゲッティを無作為に3本に折ったとき、その3本で三角形を作ることができる確率は?
この問題、なぜ難しく考える必要があるのか、私にはわからないが、すっかりイタリアンな感じの竹内薫センセの解説では、この問題を解くには、ふた通りの方法があって、まずは代数で考えたのが東大生チームだ。
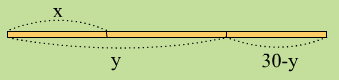
三角形の二辺の和は、他の一辺より長いので、以下のような不等式が成り立つ。
x+(y-x)>(30-y)
x+(30-y)>(y-x)
(y-x)+(30-y)>x
0<x, x<y, y<30
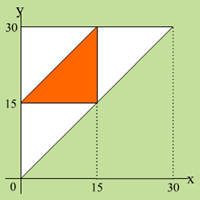
これをグラフで考えたのがマス北野だ。
同じように条件を当てはめると、x,yは、オレンジ色の部分になる。面積の比率によって、確率は1/4であることがわかる。
竹内薫センセの「美しき数学の時間」では、マーチン・ガードナーの解法を紹介していた。
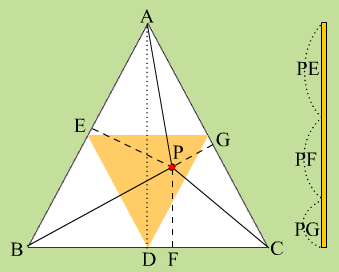
正三角形の中の任意の場所に点Pを打つ、点Pから三辺に垂直になるような線を引く。この3本の垂線の長さを合計すると、正三角形の高さになるというもの。AD=AE+AF+AG
AD=PE+PF+PG(2月16日修正)
ADを30cmのスパゲッティと考えると、AE,AF,AG(PE,PF,PG)は三つに折ったときのスパゲッティの長さになる。で、三角形の二辺の和は他の一辺より長いという条件を加えると、点Pは、オレンジ色の部分に収まっている必要があるのだ。面積比で1/4。
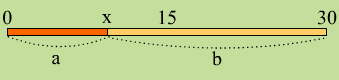
冒頭で、この問題を難しく考える必要があるのか、私にはわからないと言ったのは、最初にスパゲッティを折る場所が半分の15cmより大きくなるか、小さくなるかの確率は1/2だよね。三角形の二辺の和は他の一辺より長いのだから、次にスパゲッティを折るとき、二つに折ったスパゲッティの短いほうを選んじゃうと、三角形を作れない。長いほうか、短いほうか2本のスパゲッティのどちらか一方を選ぶ確率は、1/2なので、(1/2)*(1/2)で、三角形を作れる確率は1/4という答えになる。ふつうは、こう考えるんじゃないのかなぁ……。
2月16日追記:自分が書いた文章を読み返してみたら、2本に折ったスパゲッティの長いほうを選んでも、必ずしも、三角形が作れるとは限らない……ということに気がついた;; やはり、ちゃんと数学的に証明しないとダメみたい><;
おめぇに喰わせる「断面」は、ねえぇ!の「たけしのコマネチ大学数学科」の第37講。
問題:小さい立方体9261個を使ってひとつの大きな立方体を作り、断面が正六角形になるように切断します。このとき、小さい立方体は何個切断されるでしょうか。
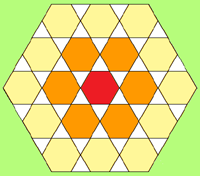
立方体の各辺の中央を通るように切断すると、断面が正六角形になる。上のFlashは、3×3×3の立方体だが、隙間を作っているので、わかりづらいかもしれない。各辺が5の立方体は図のようになる。中央の赤い六角形を取り囲むように六角形が増えていくが、小さな三角形は、六角形の数の2倍ずつ増えていく。
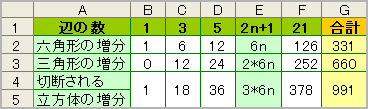
※注:表のF列の数値に誤りあり。nanzanさんのコメントを参照(2008年4月2日追記)
これを表にすると、正六角形の増分は「6n」、正三角形の増分は「2*6n」、そして切断される小さな立方体の増分は、これを足したものなので「3*6n」になる。9261個の小さな立方体で作った大きな立方体の辺の数は、21×21×21なので、これに当てはめ、合計を出す。
マス北野は、正三角形の数が正六角形の数の倍と考え、「331×2」としてしまったため、惜しくも正解を逃してしまった。1個の立方体を切断したときに出来るのは正六角形のみ。ううむ、中村亨センセの解説をそのまま、なぞっているだけになってしまった;;
美しき数学の時間では、いろいろなパターンの「アルキメデスのタイル張り」を紹介していた。最近、FlashのActionScriptで図形を描くことを覚えたので、いつか挑戦してみたい。それと、今回は、Shadeで作成したアニメーションをFlashに埋め込むことに挑戦してみた。