カテゴリー: コマネチ大学数学科

　やっと、本1冊分の原稿を書き上げ、とりあえず、重荷がなくなり、「いいちこ」な気分の「たけしのコマネチ大学数学科」の「第22回」。今回のテーマは「暗号」。問題からして、暗号なのだが、ちょっと、端折ってしまうと「マス北野の誕生日は、何曜日か？」それをアルファベットでパソコンのパスワードとして入力せよ、という問題（ちょっと演出を変えてみただけ？）。で、2006年1月1日は、日曜日で、マス北野の誕生日は「1947年1月18日」だ。

　今回の問題、エクセルなら、考える必要もなくサクサクと……。

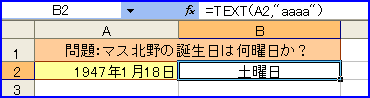
あ、コマ大数学研究会と同じ過ちを犯してしまった。英文として入力するには……。

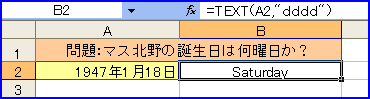
というわけだ。

　エクセルでは、1900年1月1日を「1」として、1日ずつカウントして日付を連続した「シリアル値」として、9999年12月31日まで管理している。2006年9月14日は「38974」だ。だから、ある期間の日数を求める場合は、引き算すれば、簡単に求めることができる。

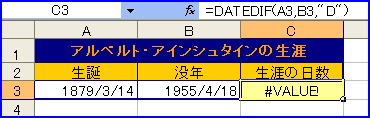
　9999年なんていう、ずっと先の未来よりも、過去の日付をちゃんと計算できるようにしてほしかったと思うのは私だけだろうか。たとえば「アインシュタイン」の生涯日数を計算しようとしても、生誕が「1900年1月1日」以前なので、エラーになってしまう。

　で、今回のテーマは「暗号」。なぜ、マス北野の誕生日の曜日を調べることが「暗号」につながるのか。竹内薫センセの「美しき数学の時間」によると、インターネット時代の公開鍵、秘密鍵を用いたRSA暗号にとって「モジュロ(MOD)」が重要なしくみを担っているということである。説明するのは大変なので、詳しくは「サルでもわかるRSA暗号」を参照してほしい。

　「モジュロ(MOD)」とは、ようするに、ある数をある数で割ったときの余り(剰余)だ。「モジュロ７をとる」と言ったら、ある数を「7」で割ったときの余り。「7を法とする世界」とも言えるようだ。つまり、この世界に「0～6」までの7つの数字しかなかったら、「6」の次は「0」になる。

　先ほど、エクセルでは1900年1月1日を「1」としていると書いたが、1900年1月1日は日曜日だ。1月2日は「2」で月曜日……1月6日は「6」で金曜日、1月7日は「7」という数字はないので「0」になって土曜日。日付が増えていっても、「=MOD(日付,7)」日付を7で割って余りを求めれば何曜日か、わかることになる。

(※2006年12月23日追記：ごめんなさい。1900年1月1日は月曜日です。Excelで日付と曜日が正しく表示されるのは、1900年3月1日以降です。)

　エクセルには、指定した日付の曜日を戻り値として返す「WEEKDAY」という関数がある。「=WEEKDAY(日付)」とすればよい。基本的に「=MOD(日付,7)」と同じ考え方なのだが、土曜日を「7」としている点が違う（その代わり「0」はない)。この関数を利用して、万年カレンダーを作ることができる。

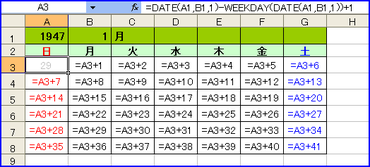
　指定した年月の最初の日「1日」が何曜日になるかを求め、それから遡って、カレンダーの最初の日曜日に表示する日にちを求める。あとは、その数に「1」を足していくだけ。

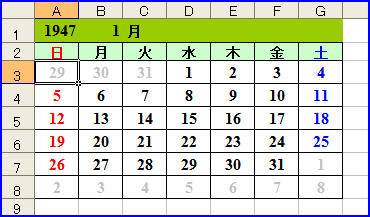
　その「月」以外の「日にち」を灰色にするには、条件付き書式で「数式が」「=MONTH(A3)<>$B$1」として、書式で文字を灰色に設定する（※セルA3はカレンダーの最初に表示する日にち、セル$B$1は、何月かを表示しているセルを指定）。

　いまさら、万年カレンダーの作り方を教えられても……なんだかなぁと思う今日この頃、いかがお過ごしですか？ とゆーか、さんざん仕事でエクセルの記事を書き、趣味のブログでもエクセルの記事を書く私は、どうかしていると思う今日この頃。もっともファミ通にいた頃は、ゲームの仕事に疲れ、息抜きに好きなゲームをしていたが……。

　ホントに頭のいい人って、自分が何をするべきかを考え、時間を使っている人なんだろうな。その場、その場で刹那的にやりたい事をやってきた私って、どーなのよの「たけしのコマネチ大学数学科」第21回。

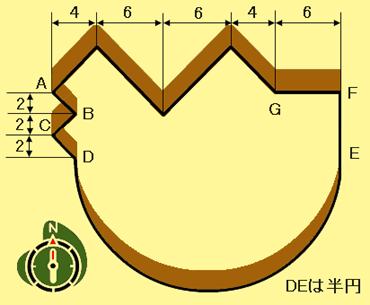
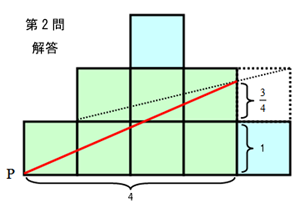
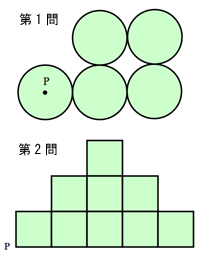　今回の講義は「等分」。第1問は、「円の中心[P]を通る直線を引き、図の面積を2等分せよ」という問題。あまりに簡単だったためか、考慮時間を残し、全員正解。というわけで、新たな問題が配られた。第2問も、同じく「角[P]を通る直線で図の面積を2等分する」問題だ。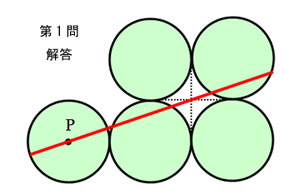
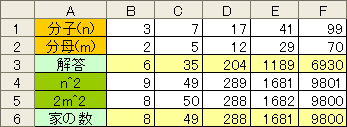
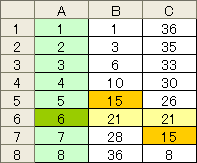　コマ大数学研究会のメンバーにとっては、晴天の霹靂だ。だって、ロケで汗を流し、巨大なノコギリで丸太を切ったのは何なんだったの？　ということになる。第2問は、いきなりロケなしのペーパーテストとなった。

　こういう図形の問題って、どういう補助線を引くかがポイントになるんだよね。でも、補助線を引こうにも限られているから、直感的に解答に辿り着く。

　第2問は、ちょっと手強い。まず、ちょっとわかりづらいかもしれないが、ブルーで色分けした2つの四角は、除外して考えても問題ない。すると、残りは7個なので、7個の四角を2等分することになる。

「(1/2)*4*X=(7/2)」の式を整えると、「X=1+(3/4)」になる。Xは、底辺が「4」で面積が「7」の四角形の高さに相当する。その対角線を結べば、面積は(1/2）になるわけだ。ポイントは補助線をどう引くかだが、マス北野は、これに苦労した。東大生コンビは計算で(1/4)と(3/4)の位置を出したが、あとは目分量で線を引いた(^^;
図は、中村亨センセの「美しき」解答。

　番組を見忘れた人のため、今回は、この他にも次のような問題が用意されていたので紹介しておく。面積を2等分することは変わらないが、右上の例題のように2つの同じ形になるようにするわけだ。図形の問題は、作図に時間がかかる。いったい私は何をやっているのか……。

　これが頭の中にひっかかっていると、仕事がなかなか進まない「たけしのコマネチ大学数学科」、許して編集者さん、懇願の「第20回」。今回のテーマは「ラマヌジャン」。

　今回、コマ大数学研究会のロケ地は、高円寺の商店街。私が放送作家なら、湾岸に並ぶ、シャッターに大きく数字がペイントされている倉庫をロケ地に選ぶな。とゆーか、この番組、放送作家は介在しているのか。それは、ともかく「10軒以上、50軒以内で1から番号の振ってある家がある。それを左右（番号の小さいほうからと、番号の大きいほう）から番号を足していき、左右が同じ数になる家の番号を答えよ」という問題。

　まずは、1番から8番までの例題を考えると、6番目の家が左右の番地を足した数が等しくなる。これを踏まえて、問題を解くわけだが、実際にロケで左右から数を足していく、数学研究会はカンタンジャンと思うかもしれない。私も力まかせにエクセルで1から50までをオートフィルで入力し、B列は上から、C列は下から足していく方法で解こうとしたが、そうは、イカヌジャン。数が合わないのだ。つまり、家の数は10以上、50以内ということで、決まっていないということ。数学研究会も、最初、そこでつまづいたが、研究会メンバーの「〆さばアタル」のひらめきで見事、解決した。

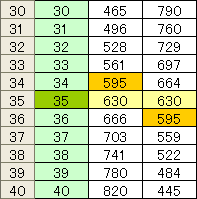　で、完全なネタばらしになってしまうが、私も数学研究会と同じ方法で正解にたどり着いた。言い忘れたが、エクセルで足し算の数式を入力する際、B列は上からなので問題ないが、C列の場合、下からとなる。エクセルの相対参照は、アクティブセルを基準にして行われるので、下から上方向のオートフィルでも問題ない。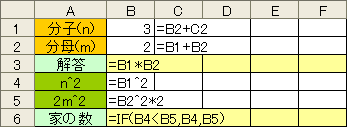

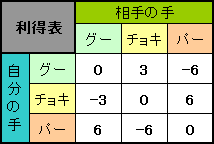　マス北野は、例題から見事な直観力を発揮して正解したが、「ラマヌジャン」は天才的な直観力を持った数学者だったらしい。竹内薫センセの「美しき数学の時間」で、今回のテーマ「ラマヌジャン」の連分数を使った解法を紹介してくれた。

　家の数が増えた場合、力まかせの数学研究会の手法では、なかなか正解にたどりつけなくなる。ラマヌジャンは、友人に「1500以内で…」という条件を加えられた問題を出されたとき、即座に「204」と答えたそうだ。竹内薫センセは、愛機「MacBook」の自作(?)プログラムで、連分数による解法の実演を見せてくれた。

　私は「連分数」のことなど、まったくわからないが、ある法則を見つけた。これなら「エクセル」だって、数が増えたときも一瞬で答えることができるぞ。

　最初の家が8軒のときの例題では、分母が「2」、分子が「3」で、答えが「2×3」で「6」になった。次が「7」と「5」で、答えが「35」だ。すると、次の分母は前の答えの分母と分子を足したもの。分子は、その分母に前の答えの分母を足したもの、と考えた。1行目の数式は「=B1+B2*2」と書き表すこともできる（こっちのほうがスマートかも）。家の数は、竹内センセの解説どおり、「分子(n)の二乗」と「分母(m)の二乗×2」と比べて、小さいほうを取る（…とココでも、法則発見）。

　この簡単な数式を入力したセルをオートフィルで入力すると、ちゃんと答えが出るじゃないですか。どうしてそうなるのか（この方法が正しいことを）証明しなさいと言われても、私にはできないけれど……。だいたい「連分数」なんて、わけがワカラヌジャン！

無限の天才―夭逝の数学者・ラマヌジャン 著者：ロバート カニーゲル 販売元：工作舎 Amazon.co.jpで詳細を確認する

　仕事に追われ、1週間遅れの「たけしのコマネチ大学数学科」第19回。今回のテーマは、昔懐かし「グリコ・ジャンケン」。

　「グリコ・ジャンケン」と言っても、若い世代の人にはわからないかもしれない。要は、ジャンケンをして、グーで勝ったら「グリコ」と3歩進み、チョキで勝ったら「チョコレート」、パーで勝ったら「パイナップル」とそれぞれ6歩進む……これを繰り返し、できるだけ進んだほうが勝ちという単純なゲームだ。

　で、問題は「グー・チョキ・パーをどのような割合で出したら、いちばんベストな手になるかを答えよ」というもの。今回、コマ大数学研究会のメンバーは、東京タワーの外階段（600段）を使って検証。ふたチームに別れ、先に上りきったほうのチームを勝ちとし、勝利チームのグー・チョキ・パーの出現割合「6:8:3」を答えとした。マス北野は「1:3:2」、東大生コンビは、最も期待値が高くなる計算で「0:1:0」と、チョキばかりを出す、見え見え作戦だった。

　「美しき数学の時間」では、中村亨センセが単純なゲームを難しい計算で解き明かし、誰もが納得する答えを導き出した。中村センセの戦法を組み込んだ「Flash」のジャンケンゲームを作ったので、遊んでみてほしい。あまり勝負が長くなっても困るので、先に「60ポイント」を取ったほうを勝ちとした。東京タワーの階段数と同じ「600」ポイント（10回勝負）をすれば、コマ大数学研究会の答えに近づくかも……。

　ノーベル賞には「数学賞」がないが、「ゲーム理論」で1994年ノーベル経済学賞を受賞した数学者「ジョン・フォーブス・ナッシュ」を題材にしたのが、映画「ビューティフル・マインド」なんだってさ。

ビューティフル・マインド 販売元：角川エンタテインメント 発売日：2005/04/28

---

　ふだん家から一歩も出ない、ひきこもり生活を送っているが、月に一度くらい、校了とか、打ち合わせのため、編集部に行く。原稿や画像の受け渡しはネットで行えるが、インターネットの時代になっても、直接、顔を合わせての打ち合わせが必要だ。しかし、めったに人ごみに出ることはないし、歩かない私にとって、かなり疲れることで、家に帰るとぐったりしてしまう「たけしのコマネチ大学数学科」の第18回。

　今回の問題は、野球選手Ａ～Ｅのデータを元に、どのポジションに割り当てたら、チームの戦力をベストにできるかというもの。データの数値は、低いほどよい。つまり、データの数値は、エラーの数と考えるとわかりやすい。

　今回もマス北野は数学的なカンを見せる。データをゴルフのスコアと見なし、最小値を「パー」と考え、各選手の最小値をデータから引く。

最小値「パー」の合計は「26」となるので、ポジションの割り当ては、いかに、この最小値に近づけることができるかが問題となる。それで、各選手のパー「0」をチェックすると、ポジション「SS」では、選手が重なり、いっぽう「外野」では誰もいない状況になる。

Ｂ選手の「3塁」は決定で、「1塁」はＣ選手にまかせてもいいだろう。問題は、「外野」を誰が務めるかである。もし、Ａ選手が「2塁」のポジションをとったら、Ｄ選手か、Ｅ選手が「外野」をやらなければならなくなり、どちらも「＋3」でチームにとっては、ありがたくない。Ａ選手が「外野」をやってくれれば、「＋1」で収まる。残る「2塁」と「SS」だが、Ｄ選手が「2塁」をやると「＋3」になってしまうので、Ｅ選手が「2塁」（＋1）、Ｄ選手が「SS」ということで、チームとしては、ベストなポジション割り当てになる。

　中村亨センセの「美しき数学」では、さらに手順を追加し、確定的にポジションを決定できるようにデータを組み立て直していたが、私としては、マス北野の「パー」と「ハンデ」という考え方のほうがわかりやすかった。

　こういった考え方は、現実の問題として広く使われているようだ。番組では「線形計画法」が紹介されていた。中村亨センセの言うとおり、選手が５名の場合は、選手のポジションの組み合わせは、５の階乗で120通りだが、選手が10名になると、3,628,800通りにもなる。力まかせに、すべての組み合わせを実行し、最小値を求めるやり方では効率が悪い。そこで、いろいろなアルゴリズムが考えられているという。

　ところで、関係のない話だが、あるブログで「編集者Blogはナゼ滞るのか？」という記事を目にしたが、その理由として……

１．通常業務が忙しいので書けない。 ２．編集後記ノリのヌルイ内容では厳しい批判に晒されるので書けない。 ３．特に主義主張がある訳でもなく書くべき事が無いので書けない。 ４．給料が増える訳でも講演依頼が来る訳でも無いので馬鹿らしくて書けない。 ５．編集長も書いてないから．．．。 ６．怠け者の家系なので．．．。

　……と理由を挙げていた。もちろん、これには「ライター」の立場は含まれていないが、「ライターのブログはナゼ更新が滞るのか？」ということならば、それは「編集者が見ているから」という項目を付け加えたい。もし私が編集者の立場なら、お金を払って原稿を依頼しているのに、その原稿の締め切りを守らずに、一銭の得にもならぬ、ブログの記事を書いている。「そんな時間があるのなら、1時間でも、1分1秒でも早くこちらの原稿をアップしろ！」と思うのがトーゼンだ。やはり怒りますよ。つまり、ブログの更新ができるのは、ちゃんと締め切りを守っているライターのみ……とゆーか、少なくとも、修羅場ではない状況、人間関係が壊れない状況ということなんだよね。

　「たけしのコマネチ大学数学科」第17回のテーマは「エッシャー」だった。例題として「ペンローズの三角形」が登場したが、少しペンロースに関して補習しておこう。エッシャーとペンローズは、互いに影響を与え、つながりがあったようだ。エッシャーの絵に触発されたペンローズが作ったパラドクシカルな三角形が「ペンローズの三角形」だ。

　ロジャー・ペンローズの父は遺伝学者の「ライオネル・ペンローズ」。祖父は肖像画家で、父も絵の才能に恵まれ、インク画や油彩を描いていたそうだ。ペンローズが例の三角形の絵を父に見せると、父は興味を示し、さまざまな不可能物体や不可能建築の絵を描き、やがて、どこまでも上り続ける階段を作った。ペンローズと父は、その描いた絵のコピーをエッシャーに送り、エッシャーはそれをさらに発展させ「上昇と下降」という作品に結実させた。また「滝」も、ペンローズの三角形をベースにした作品だという。
（参考：[対談]ロジャー・ペンローズ＋佐藤文隆）

　ペンローズといえば、「ペンローズのタイル」が有名。下の図は二種類のタイルを組み合わせて、平面充填していくもの。無限に細分化していくことが可能であることから、無限の平面を充填できることになる。しかも、タイルの組み合わせが反復しない。
（参考：さんすう・数学）

　この非反復性の「ペンローズのタイル」をエッシャーは見ることなく他界した。

　「貧乏ヒマなし」は、あまりありがたくはないけど、貧乏でヒマになってしまうと、生活もできなくなって、もっと困る。働けど働けど我が暮らし楽にならず、じっと手を見る「たけしのコマネチ大学数学科」の第17回。

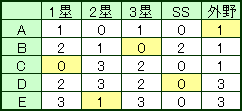
　まずは例題。左の図は「ペンローズの三角形」。実際にはありない形をしているが、ある位置から眺めると、このように見える図形を作ることができる。

　またまた「Shade」で作ってみたのが、こんな図形。カメラ位置を調整して、普通のレンズだと遠近感がついてうまく重ならないので、並行投影すると、「ペンロースの三角形」に見える。

　今回の問題は、ある角度から見たとき、下の図のように見える図形を作りなさいというもの。

　これはエッシャーの「ベルベレーデ（物見の塔）」にも登場する図形だそうだ。今回は、どんな方法でも、上の図形に見えればいい。非常にユニークな解答をしたのが数学研究会のメンバーだった（不正解だったけど）。東大生チームは、解答へ辿り着く方法はマス北野と同じだったが、雑な作りなためフィールズ賞を逃した。

番組で竹内薫センセが紹介していた本がおもしろそう。

「ゲーデル、エッシャー、バッハ – あるいは不思議の環」

中心となっているテーマは「自己言及」だが、これが数学におけるゲーデルの不完全性定理、計算機科学におけるチューリングの定理、そして人工知能の研究と結びつけられ、渾然一体となっている。エッシャーのだまし絵やバッハのフーガはこれらをつなぐメタファーとして機能している。

出典: フリー百科事典『ウィキペディア（Wikipedia）

ゲーデル、エッシャー、バッハ ―あるいは不思議の環 20周年記念版 著者：ダグラス・R. ホフスタッター 販売元：白揚社

---

　曙太郎が不甲斐なくダウンしたり、亀田興毅が不甲斐なくダウンしたり、一週間は瞬く間に過ぎて「たけしのコマネチ大学数学科」の第16回。

下図のような周りを同じ高さの塀で囲ってある土地がある。真南から太陽が照りつけ、２ｍの長さの影ができた。このときの影の面積は？

　酔っ払った頭では思考力がゼロ。ただ、ぼーっと番組を眺めていただけで、考えようともしなかった。東大生チームは完璧な解答。マス北野も問題を単純化する直観力は見事だなぁ……。２ｍの影ができるということは、図形を２ｍ並行移動したことと同じ。つまり東西方向の幅に平行移動させた２ｍを掛ければ面積がでる。ただし、ＡＢＣＤの部分では影が重なるので、その分を引いてやらなければならない。

　中村亨センセの「美しき数学の時間」では、山手線（全長34.5Km）のレールとレールの間の面積を求める方法も紹介された。

線路名称の「山手線」は、品川駅から、渋谷駅、新宿駅、池袋駅を経由して田端駅までを結ぶ、全長20.6kmの路線の名称。 　運転系統の「山手線」は、上記の山手線路線「品川駅～田端駅」に加え、東北本線の「田端駅～東京駅」、東海道本線の「東京駅～品川駅」を合わせて環状運転を行なう運転系統の名称。起点の大崎駅から、大崎駅まで戻る環状線1周の距離が34.5kmで、所要時間は約60分。一般的に、山手線といえばこちらの意味で使われていることが多い。

http://www.rbbtoday.com/column/mtakaya/20050420/

　「なるほど～」というわけで、中村亨センセによると、面積を求めるには、全長にレール幅を掛ければ求めることができる。なぜ、そうなるかは、ココのサイトを見てほしい。
http://www.nikonet.or.jp/spring/sanae/MathTopic/obi/obi.htm

　ＪＲ在来線のレール幅は1067mmなので「34500×1.067＝36811.5㎡」ということになる。中村亨センセは「線路が右にカーブしようが、左にカーブしようが、微分していくと台形になり、台形の面積を求める「(上底＋下底)÷２×高さ」の「(上底＋下底)÷２」は、レールとレールの間の中央になり、高さはレール幅になる。全長というのは、レールとレールの中間を計測しているはずだから……」と言うけれど、山手線って内回りと外回りの複線だよね。全長といったとき、どちらを計ったのだろう。もし、内回りと外回りのレールの中間なら、かなり誤差が出てくるんじゃないかと気になってしまった……。我ながら、ベタなツッコミで、申し訳ない（＞＜；

　締め切りに追われつつも、やはり見てしまう「たけしのコマネチ大学数学科」。今回の問題は「1辺10cmの正方形のタイルをしきつめた床に直径3cmのコインを落としたとき、4つのタイルに重なる確率は？」

　もう「エクセル」はあきらめて、「Flash」で作ってみた。プレイボタンを押すと、数学研究会と同じく「1010回」コインを投げる。