関東ローカルかもしれないけれど、火曜深夜にTBS系列で「ネプ理科」という番組をやっている。先日は、このブログでもとりあげた「誕生日」問題をやっていた。スタジオ内にいるスタッフを含めた58人の中に誕生日が同じ人がいる確率は? というもの。めでたく実際に同じ誕生日のカップル(たまたま、男性と女性の組み合わせだった)が誕生した。人数が58人くらいになると、誕生日が一致する確率は、約99%になるんだよね。
で、同じく「ネプ理科」でとりあげられていた「数当てゲーム」がある。深夜の番組らしく、女性に「過去に付き合った男性の数」を思い描いてもらい、数字が並んだ一覧表の中にその数が「ある」か「ない」かを答えていき、その数を当てるというもの。番組では、0~63の数でやっていたけれど、もう少し簡素にして0~15の数を当てるFlashゲームを作成してみた。
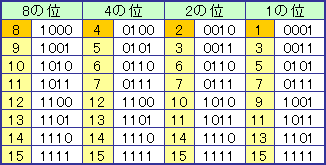
番組では、その仕組みを詳しく解説していなかったが、これは、二進数を使い、位ごとにビットが立っている状態を調べるとすぐわかる(二進数は、0か1で表すので、1の場合、ビットが立つと言う)。上のFlashゲームでは、赤いランプを「1」、青いランプを「0」とすると、そのまま、二進数表記になっている。以下は、十進数と二進数の対応表。
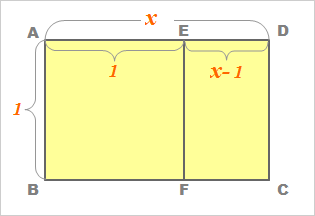
この4枚の数字が並んだカードを見せ、「ある」と答えたカードの最初の数を足した数が、思い描いた数になる。たとえば、2の位と8の位に「ある」と答えたなら、「2+8」で「10」ってわけ。思い描いた数が「15」の場合は、すべて「ある」と答えることになり、二進数で表すと「1111」になる。つまり、4ビットで表すことのできる最大の数だ。「ネプ理科」では、これを6ビット(6枚のカード)でやっていたのだが、「過去に付き合った異性の数」という設問だと、「15」では足りないと思ったのかな^^;
ところで、この「数当てゲーム」は、以前、NHK教育の高校講座「数学基礎」という番組で、秋山仁センセが、その仕組みを解説していた。とゆーか、数の表し方「二進数」の勉強のために「数当てゲーム」を使って説明していたというほうが正しい。この番組では、さらに3枚のカードを加え(4枚+3枚)で、カードの中に選んだ数字が「ある」か「ない」かを答える際に、1回だけ嘘を言ってもよいというルールを追加している。嘘をついても数字が当てられるのは、パリティチェック(parity check)という手法で、嘘をついたカードを見つけ、正しい数に訂正できるからだ。こういった誤り検出訂正の符号理論は、CDやDVDなどは、もちろんのこと、ネットワークで情報を送受信するときなど、私たちがいつもお世話になっている技術の基礎となっている。
番組を見逃した方や、もう一度、高校生と一緒に、秋山仁センセの授業を受けたい人は、インターネットで受講できるよん(「番組を見る」で動画再生)。
■NHK高校講座「数学基礎」数の表し方