■コマ大数学科166講：オクタゴン

今回のテーマは、オクタゴン。オタクゴンではないよ「たけしのコマ大数学科」

問題：1辺の長さが1の正八角形の周上を3点P,Q,Rが動くとき、△PQRの面積の最大値を求めよ。

ガスコン爺が作成したFlashでは、3点P,Q,Rの動かせる範囲が限られているし、各点をドラッグして動かしたあと、うまくドロップできないことがあるが、勘弁してほしい＞＜；

●コマ大生の検証

コマ大数学研究会は、グーグルアースで正八角形の建物を検索。名付けて「コマ大世界遺産」。

(C)Google Maps

で、この上空から見た建物を三角形に切り抜いて、精密計量器で重さをはかる検証なのだが、計量する機器は精密であっても、切り抜く手作業の部分は、どう考えても精密さに欠ける。さらに根本的な問題は、重さを求めることではなく、面積を求めることだ＾＾；

コマ大生の答えは「0.461g」

●マス北野＆ポヌさん

三角形の面積は、底辺×高さ÷2なので、最大の面積を得ようとすると、底辺も高さも大きい方がよい。しかし、最大の高さを求めると、底辺は小さくなり、逆に底辺を最大にすると、高さが小さくなる。マス北野は、図1のような、2つ三角形を描き、ポヌさんに、どちらの三角形の面積が大きいか計算してもらう。

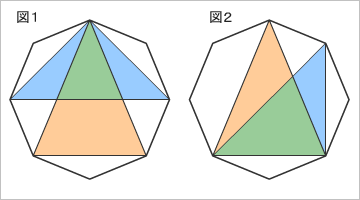
しかし、青い三角形を回転させると、計算するまでもなく、見た目でオレンジの三角形の面積が大きいことがわかる。じつは、このオレンジの三角形が最大の面積になる。あとは、正しく面積を計算することができればよいのだが……。

マス北野＆ポヌさんの答えは「2+√3」

●東大生（木村美紀＆山田茜さん）

証明の過程は不明だが、東大生チームは、下図のような三角形が最大の面積になるとして、その面積を求める方法を考えた。

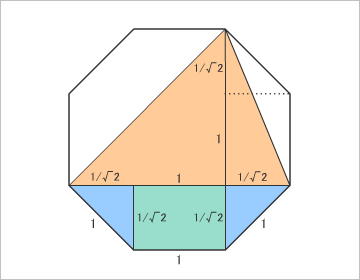
n角形の内角の和は（180×n－360）なので、正八角形の内角の和は（180×8-360＝1080）、ひとつの内角は（1080÷8＝135）。そこから90度を引くと（135－90＝45）。つまり、青い三角形は、二等辺直角三角形。正八角形の一辺は「1」なので、除く他の二辺は（1/√2）になる。すると、オレンジの三角形の面積は「底辺(1＋2×(1/√2))×高さ(1+(1/√2))÷2」、これを計算すると……。

東大生の答えは「1+3√2/4」

★正解は「1+3√2/4」で、東大生がコマ大フィールズ賞を獲得した。ちなみに、小数で表すと「1+3√2/4≒2.060660171779821」

●竹内薫センセの「美しき数学の時間」

三角形の面積が最大のとき、三角形の各頂点が必ず、正八角形の頂点と重なる。これを厳密に証明しようとすると、大変なようである。

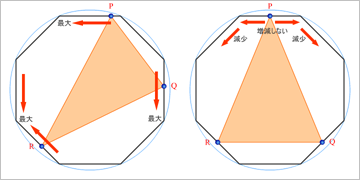
でも、冒頭のFlashで遊んでみれば、頂点以外では面積が最大にならないことは明白。正八角形の辺に任意の3点を取る。たとえば、辺RQを固定して、点Pを正八角形の周上を移動させると、頂点が面積の最大になる。これは、辺PRを固定しても、辺PQを固定しても、同じことが言える。例外として三角形の底辺が正八角形の一辺と並行だった場合、残る1点を移動させても、面積が変化しないことがある。

各点が辺上にある限り、その点を移動させると、面積は連続的に増加、あるいは減少する。増加から減少に転じるのは頂点であり、最大となる（前述したように変化しない場合はある）。

たぶん、これを数式で表し、証明するのは大変だということだと思う。

●ガスコン爺の≪番外編≫
爺はどのようにして三角形の面積を計算しているか

(※A,B,Cの各点をドラッグ＆ドロップしてみてね）

「たけしのコマ大数学科」には、図形の面積を求める問題が時折、登場するが、ここでは、代数的な求め方ではなく、コンピュータ（Flash）を使って、数値的な近似値を求める方法を紹介しよう。FlashのAction Scriptを学ぼうとしている人にしか興味がない話かもしれないので、興味がなければ読み飛ばしてほしい。

三角形の一辺を底辺と決める（上のFlashでは、BCを底辺としている）。残りの頂点（A)から、辺（BC）に垂線の足を下ろせば、高さが求まるので、底辺×高さ÷2＝面積となるが、問題は、辺BCと交わる垂線の足の位置をどのように計算するかだ。

上は、その主要な関数の部分を抜き出したものだが、Flashには、「Point」という便利なクラス（組み込み機能）がある。たとえば、「A」というポイントを設定すると、そのX座標とY座標を保持する。

「Point」を使わないと、上にあるような、ややこしい座標計算をしなくちゃならない。Pointを使うと、たとえば、2点間の距離を求める場合は「kyori = Point.distance(B,C)」と記述すれば計算してくれる。また、垂線を引くとき、便利なのは、「Point.ineterpolate」というメソッド（操作手続き）だ。これは、BC間の距離を「1」として、その線上にある、Bからの距離（0～1：値が負、1より大になっても可）のX座標、Y座標を返す。

とにもかくも、爺は「たけしのコマ大数学科」の問題を解くのも愉しみだが、その問題をFlashで作るのも楽しい＾＾；

で、爺は「Flash CS4」を持っているんだけれど、未だに「Flash 8」を使うことが多い。Flash 8は、ActionScript2.0（AS2)で、CS4は、AS2とAS3のどちらのファイルも作成可能（ただし、ファイルの保存形式はFlash8との互換性はない）。AS2とAS3では、まったく別物と言っていいほど違う。ついつい、使い慣れた、いい加減さが許される、AS2の楽な方へ逃げてしまうんだよね。歳をとると、新しいものに順応できなくなる証拠か……これじゃ、いかんと思い立った次第。これからは、試行錯誤しながらも、少しずつAS3の作法を覚えていこうっと＾＾；

※ソースのダウンロード
Vertical_as2.zip（Flash 8以降）
Vertical_as3.zip（Flash CS4）

※コマネチ大学数学科の「過去問題」はこちらから。
■コマ大数学科：2008年度全講義リスト
■コマネチ大学数学科：2007年度全講義リスト
■コマネチ大学数学科：2006年度全講義リスト

---