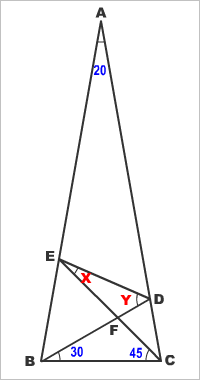
今回は、視聴者から寄せられた「謎の難問」から始まった「たけしのコマ大数学科」。なんでも、投稿者のKさんによると、中学のとき、この問題に出会い、以来30年間、解けぬままだと言う。要は、XとYの角度を求めればよい。
そこで、我らが「コマ大数学研究会」の面々が立ち上がった。向かったのは、東大進学コースのカリスマ数学講師、河合塾の「岡田順一」講師だ。
問題を見るなり、「いわゆる、ラングレーの問題と言われるタイプ」と見抜く。黒板にすらすらと式を書いていく岡田講師。しかし、岡田講師をもってしても「X,Yの角度はコンピュータを使わないと無理」と言われてしまう。
コマ大生の頭の中に、コンピュータに勝る、ある男の姿が浮かんだ。現役東大生にして、数学オリンピック金メダリスト、初代マス1グランプリの覇者、西本将樹さんだ。
じつに楽しそうにニコニコしながら、問題を解く、西本将樹さん。しかし、西本さんにも、式は立つのだが、具体的な答えとなると、「整数や分数ではなく、人間が簡単に書き表せる数ではない」と言われてしまう。
河合塾の岡田講師が黒板に書いた式をエクセルで計算してみた。

※注意:「エクセル」で三角関数を使うときは、度数ではなく、ラジアン値にする。
よーするに、岡田講師や西本さんの言うように、答えが半端な数になってしまうわけだ。じつは、「ラングレーの問題」は、10度単位の問題に関しては、スパッとした答えが出ることが証明されているらしい。しかし、「謎の難問」は、この角度が「45度」と10度単位になっていないことが原因らしい。
というわけで、今回は「謎の難問」を解くことではなく、次のような問題。
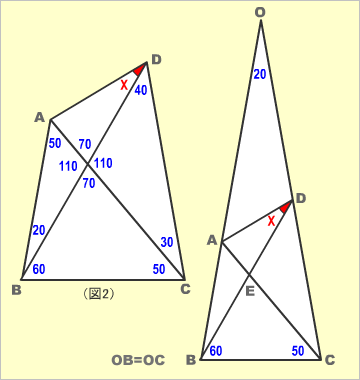
(図2)は、問題図の一部を抜き出したもの。パッと求めることのできる角度を書きこんでおいた。しかし、これだけでは、Xの角度を求めることができない。ここから先が問題なのだ。
マス北野&ポヌさんチーム、衛藤樹さん&伊藤理恵さんの東大理科三類「秒殺シスターズ」が苦戦する中、コマ大生チームは、すらすらと答えを書き出した。計算方法は……と見てみると、なんと「分度器」で測っている^^; それは反則技だってば><;
ここで、中村亨センセから重要なヒントが出る。
この補助線のヒントがあれば、あとは、簡単だ。しかし、マス北野は、簡単な足し算、引き算を間違えてしまい、「40°」という答え。あわてて、答えを消したが、時すでに遅し。東大生チームは「30°」という答えで、もちろん正解。コマネチ・フィールズ賞を獲得。
中村亨センセの「美しき数学の時間」では、別の解法も紹介された。
エドワード・マン・ラングレー(1851~1933)は、数学教育に熱心なイギリスの学校の先生だったらしい。いわゆる「ラングレー問題」は、10の倍数となるような角度の場合、コンピュータを使い、350以上の解が見つかっている。それぞれの問題に対し、どんな補助線を引いたらいいのか、興味深い。
※6月20日追記
■ABOUTさんの解答(※コメント参照)

たけしのコマ大数学科#93
たけしのコマ大数学科#93
(旧名称・たけしのコマネチ大学数学科)
フジテレビ 2008年6月19日 深夜OA
今回のテーマは、
「謎の難問」
DVDBOX第2期発売:2008年07月16日
【New!! DVD】
たけしのコマ大数学科DVDBOX 1
¥5,284
【New!!…
いつも楽しく拝見しています。
今回の問題は以前友人たちと考えた解法があるので、勝手ながら書かさせていただきます。
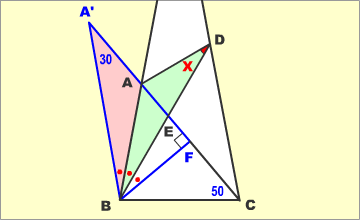
BDと等しい長さの直線をABから左側に20°のとこに引き(A´B)
同様にBDから右側に20°のとこに引きます。(BD´)
ACとBD´の交点をFとすると
∠BFE=180°-(∠BEF+∠EBF)=90°
となります。
A´とFを直線でつなぎます。
すると,∠BA´F=180°-(∠A´BF+∠A´FB)=180°-(60°+90°)=30°
となります。
三角形AA´Bと三角形ADBについて
ABは共通
A´B=DB
∠ABA´=∠ABD
よって,三角形AA´B≡三角形ADBとなります。
したがって,∠BA´A=∠BDA´
となるので,∠BDA´=30°
という解法があります。いかがでしょうか?
初めての書き込みで長文失礼しました。
ABOUTさん、コメントありがとうございます。
素晴らしい解法だと思います。図がないとわかりにくいので、記事中に図を載せておきました。
たけしのコマ大数学科:謎の難問、ですとぉう?!\(^o^)/
たけしのコマ大数学科:謎の難問、ですとぉう?!\(^o^)/ 6月20日(金)(フジTV 1:15-1:45am)の「たけしのコマ大数学科」は 視聴者から寄せられた「謎の難問」(三角形幾何)がオープニングでした。 問題、番組内容はいつものようにこちらのお二人のBLOGを参照ください。 コマネチ大学数学科94講:謎の難問 from 「ガスコン研究所」BLOGさん http://gascon.cocolog-nifty.com/blog/2008/06/94_dfaf.html#more 「シャ…
ABOUTさんの解法に対する素朴な質問なんですが、、、AがA'F上にある事の説明は必要ないのでしょうか?
ABOUTさんとほとんど同じです。
しかし、垂線はありません。
CAを延長させ、△A'BAをつくって
△ADEの外角の性質から
70+x=(20+x)+(20+x)
x=30°としました。
正解と言ってもいいですか??
∠ADB=x°とし
CAを延長させ、
点A'をとり、△DABと合同な
△A'BAをつくって
△ADBの外角から
70+x=(20+x)+(20+x)
x=30°としました。
なんどもすいません。
最初の解法、
【∠ADB=x°とし
CAを延長させ、
点A'をとり、△DABと合同な
△A'BAをつくって
△ADEの外角から
70+x=(20+x)+(20+x)
x=30°としました。】
をみてください!
こんな昔の回へのコメントで失礼します。
>じつは、「ラングレーの問題」は、10度単位の問題に関しては、スパッとした答えが出ることが証明されているらしい。
とありますが、残念ながらそれは誤りです。(反例はすぐみつかります。)
正しくは
「10°単位の問題で、スパッとした答えが出るものについては、その答えとなることを初等幾何だけで証明できる」
となります。
実を言うと、
「5°単位の問題で、スパッとした答えが出るものについては、その答えとなることを初等幾何だけで証明できる」
「3°単位の問題で、スパッとした答えが出るものについては、その答えとなることを初等幾何だけで証明できる」
ということも言えるので、10°単位でないからきれいな答えにならないというのも理由になっておらず、実際は、単に「その角度の組合せはきれいな答えにならない組合せである」ということにすぎません。
番組を30分に編集する都合もあると思いますが、この手のミスリードはこの番組ではしばしばあるので、(番組批判という意味ではなくサポートという意味で)気づいた間違いはこういう場で修正するのも有意義だと思います。
ついでに、「スパッとした答えが出る」ラングレーの問題の類題をランダムに出題するFlashコンテンツを紹介しておきます。
http://www.gensu.co.jp/saito/kikadaiou/
jerseyboyさん、ガウスさん、コメントをいただきながら、長い間、何も答えることができなくて、申し訳ないです。
番組が放映され、記事を書くときは、爺も自分なりに一所懸命考えるのですが、なにせ、数学の素養がないので、わからないことだらけです。それに、しばらくすると、覚える先から忘れていってしまうんですよね。ちっとも身についてない><;
dobaさん、コメントありがとうございます。
爺は、ほんとに勘違いや、多くの間違いをします。数学を専門に学んでいる人や、数学が得意な人が、間違いを指摘してくれたり、フォローしていただけると、大変助かります。
随分と遅いコメントで申し訳ありません。
ABOUTさんの
「三角形AA´Bと三角形ADBについて
ABは共通
A´B=DB
∠ABA´=∠ABD
よって,三角形AA´B≡三角形ADBとなります。」
の辺の長さが等しいことが証明されていないように思いますが・・・
この問題は私は中に正三角形を作図する方法で30度であることを示しました。