録画しておいた「たけしのコマネチ大学数学科」を見る。今回の問題は、アインシュタインが晩年、新聞に連載していたものらしい。「図のA~Iの□の中に1から9までの数字を1つずつ入れ、7つの三角形の3つの頂点に入る数の和がすべて等しくなるようにしてください」
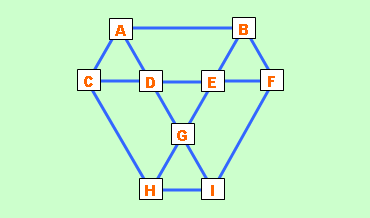 「ACD」「BEF」「DEG」「GHI」の小さな三角形の他に「ABG」「CEH」「DFI」の大きな三角形を合わせて7つということ。それぞれの頂点に入る数の和が等しくなるようにする。このブログの「六芒星のパズル」でも紹介したが、まず、3つの数の和がいくつになるかを考える。1~9をすべて足すと「45」、それを3で割ると、「15」になる。
「ACD」「BEF」「DEG」「GHI」の小さな三角形の他に「ABG」「CEH」「DFI」の大きな三角形を合わせて7つということ。それぞれの頂点に入る数の和が等しくなるようにする。このブログの「六芒星のパズル」でも紹介したが、まず、3つの数の和がいくつになるかを考える。1~9をすべて足すと「45」、それを3で割ると、「15」になる。
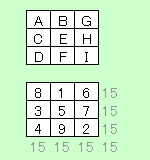 で、このパズル、3×3マスの「魔方陣」として考えると、容易になる。ここが今回の「美しき数学」のポイントなのだろう。ここで図の「DEG」は、3つの三角形の頂点になる。他の点は2つの三角形で使われる。これを魔方陣で考えると四隅は3回、中央4回、その他2回になる。つまり対角線の組み合わせは「8、5、2」か「6、5、4」になる。四隅と中央が決まれば、あとは残りの数字を当てはめていくだけだ。
で、このパズル、3×3マスの「魔方陣」として考えると、容易になる。ここが今回の「美しき数学」のポイントなのだろう。ここで図の「DEG」は、3つの三角形の頂点になる。他の点は2つの三角形で使われる。これを魔方陣で考えると四隅は3回、中央4回、その他2回になる。つまり対角線の組み合わせは「8、5、2」か「6、5、4」になる。四隅と中央が決まれば、あとは残りの数字を当てはめていくだけだ。
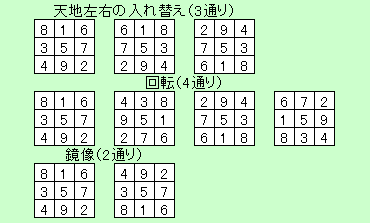
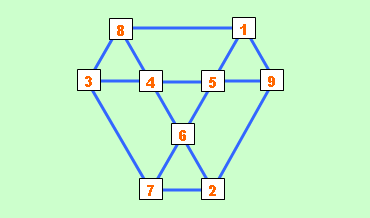 「マス北野」は、いちはやく正解にたどり着き、正解のパターン数、つまり「何通りの答えがあるか」について悩んでいたようだが、入れ替え3通り、回転4通り、鏡像2通りで、3×4×2で「24通り」。
「マス北野」は、いちはやく正解にたどり着き、正解のパターン数、つまり「何通りの答えがあるか」について悩んでいたようだが、入れ替え3通り、回転4通り、鏡像2通りで、3×4×2で「24通り」。
※2010年4月11日追記:これはあくまで3×3の魔方陣の場合で、アインシュタインの魔方陣にはあてはまらないようだ><;
 ところで、今回の「魔方陣」を9個並べると、「数独」(ナンバープレイス)と呼ばれるゲームになる。こちらは、3×3マスの中には、1~9の数字が入るだけで、足して「15」になる縛りはない。しかし、列、または行においても、1~9の数字が入り、同じ数字が重複してはならない。
ところで、今回の「魔方陣」を9個並べると、「数独」(ナンバープレイス)と呼ばれるゲームになる。こちらは、3×3マスの中には、1~9の数字が入るだけで、足して「15」になる縛りはない。しかし、列、または行においても、1~9の数字が入り、同じ数字が重複してはならない。
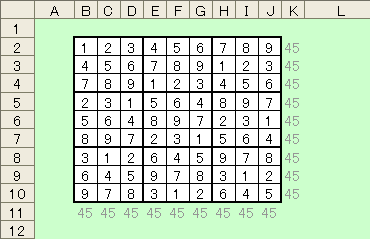 この場合「B、C、D」「E、F、G」「H、I、J」の各列、「2、3、4」「5、6、7」「8、9、10」のそれぞれの各行を入れ替えることが可能、また3×3マスを1ブロックとした場合、縦のブロック、横のブロック単位で入れ替えることも可能だ。
この場合「B、C、D」「E、F、G」「H、I、J」の各列、「2、3、4」「5、6、7」「8、9、10」のそれぞれの各行を入れ替えることが可能、また3×3マスを1ブロックとした場合、縦のブロック、横のブロック単位で入れ替えることも可能だ。
「数独」の問題の中には、稀にこのようにパターンを入れ替えただけの問題も含まれることがあるようだ。
番組の最後には、自ら「アインシュタイン」マニアと称する竹内薫センセの著書「アバウトアイシュタイン」(アインシュタインをめぐる70のミステリー)の中から、エピソードを紹介していた。30分番組ということで、途中でカットされてしまっていたが……;;。
 アバウトアインシュタイン ―アインシュタインをめぐる70のミステリー 著者:竹内 薫 |

「数独」って面白いゲームですよね。
収録では3話くらいしゃべったんですが、まあ、解説のほうが大切ですから。
拙著を紹介していただき、感謝です。
「数独」は「ニコリ」の登録商標で、一般には「ナンバープレイス」(略して「ナンプレ」)と呼ばれていますが、イギリスの新聞で連載されるなど「SUDOKU」という呼称は世界的に有名になりましたね。
「たけしのコマネチ大学数学科」は深夜番組としては、驚異的な高い視聴率を獲得し、1年は続くとのこと。毎回、問題選びにも大変なご苦労があると思いますが、これからも驚きの「美しき数学」の時間に期待しています。
■数独の解は何通りか?
「たけしのコマネチ大学数学科」は深夜番組なので、放映時間まで、焼酎「いいちこ」を飲みながら、数学の問題を解いて、頭を数学モードにしようと試みてみるが、たいていは、番組が始まる前に酔いつぶれてしまう><; で、今回は、「数学オリンピック2000-2005」という本からの出題。 問題:4×4のマス目を作り、1から4までの数字をそれぞれ4つずつ書き込む。ただし、以下の条件を満たすものとする。1:各行には…
この問題が懐かしくなり久々にといておりました。
ところで天地左右の入れ替えって何ですか?天地左右の入れ替えの3番目を180°回転させると元に戻ってしまう気がします。
番組解説では、無限循環の魔方陣をGED方向(右上又は左下)にスライドさせるんではなかったでしたっけ?
通常の魔方陣は和を8組使うのに対してアインシュタインの方は7組なので、
AEI、FGC、HDBの3つは生かされないことを利用して。。。
816 735 924
357 -> 249 -> 168
492 681 573
たしかこんな感じだった気がするのですが
いかがでしょうか?
もちろんこの場合左上から右下への合計は崩れますが、アインシュタインの魔方陣ではこの方向の和は使いませんので問題ないと思います。
4年近く前の問題を掘り返すようで申し訳ありません。
muさん、コメント&間違いの指摘ありがとうございます。また、返事が遅れて申し訳ないです。
記事中に注釈を入れました。