2014年冬季オリンピック開催地はロシアのソチに決定した。韓国の平昌(ピョンチャン)は、2010年の冬季オリンピックに続き、またしても決選投票で涙を飲む結果となった。そんな国際オリンピック委員会(IOC)とは、まったく関係のない「たけしのコマネチ大学数学科」の第53講。今回のお題は、2001年国際数学オリンピック(IMO)の予選問題。
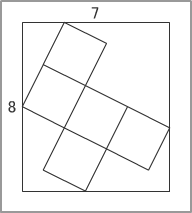 問題:縦が8、横が7の長方形の中に図のように5つの合同な正方形が詰め込まれている。正方形の1辺の長さを求めよ。 |

What are you studying?
2014年冬季オリンピック開催地はロシアのソチに決定した。韓国の平昌(ピョンチャン)は、2010年の冬季オリンピックに続き、またしても決選投票で涙を飲む結果となった。そんな国際オリンピック委員会(IOC)とは、まったく関係のない「たけしのコマネチ大学数学科」の第53講。今回のお題は、2001年国際数学オリンピック(IMO)の予選問題。
 問題:縦が8、横が7の長方形の中に図のように5つの合同な正方形が詰め込まれている。正方形の1辺の長さを求めよ。 |
「たけしのコマネチ大学数学科」は深夜番組なので、放映時間まで、焼酎「いいちこ」を飲みながら、数学の問題を解いて、頭を数学モードにしようと試みてみるが、たいていは、番組が始まる前に酔いつぶれてしまう><;
で、今回は、「数学オリンピック2000-2005」という本からの出題。
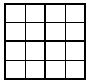
問題:4×4のマス目を作り、1から4までの数字をそれぞれ4つずつ書き込む。ただし、以下の条件を満たすものとする。
1:各行には、1,2,3,4が1回ずつあらわれる。
2:各列には、1,2,3,4が1回ずつあらわれる。
3:全体を図のように太線で4つの部分に分けたとき、各部分に1,2,3,4が1回ずつあらわれる。
このような数字の書き込み方は何通りあるか。
昨日の「たけしのコマネチ大学数学科」は、特番が入り、休講だった。そこで、過去の「数学オリンピック」で出題された問題を考えてみたいと思う。
問題:一泊500円のホテルがあり、そこに500円玉を持った、n人の人と1000円札しか持っていない、n人の合計2n人の客を泊らせたい。ホテルの受付は受付開始時には、つり銭を準備していないとする。つり銭が不足しないような客の来かたは全部で何通りあるか。
数学の問題は、時としてシュールだ。ホテルと名前はついているものの、一泊500円と格安。秋山仁センセのような風体をした日雇い労働者たちが、500円玉、あるいは1000円札を握り締め、その日の宿を求め、列をなしている光景を想像してしまう。百円玉や10円玉を握り締めている人がいないのは、なぜなのか……問題とは、まったく関係のない妄想が広がる。
で、一般項(n)を求める問題は難しいので、とりあえず、500円玉を握り締めている人が5人、1000円札を握り締めている人が5人、総計10人で考えてみる。普通に考えると、500円玉(つり銭不要)の人と1000円札(つり銭必要)の人を2列に並ばせ、つり銭不要の人を優先して受け付ければ問題ないと思う。まあ、この問題は、これらの人たちが1列に並んでいると考える。この並び方が何通りあるかを考えるというものだ。最初のお客は、当然、つり銭がないので500円玉を握っている人だ。
まったくランダムに10人が1列に並んだとき、その並び方の組み合わせは、10×9×8……×1で、10!(10の階乗)で360万通りにもなる。でも、この組み合わせの中には、当然、つり銭が払えない場合も含まれる。
そこで、500円玉の5人と、1000円札の5人の2つのグループに分けて考える(当然だよね)。受付の人にとっては、Aさん、Bさんという個人が問題なのではなく、500円玉を握り締めているか、1000円札を握り締めているかが問題だ。
ふたつのグループを表にしてみた。X軸は500円玉の人、Y軸は1000円札の人……。でも、つり銭が足りなくなっては困るので、X軸(500円玉)≧Y軸(1000円札)というルールを適用する。つまり、1000円札の客を受け付けるのは、つり銭があるときだけ。このルールを適用するだけで、表の半分は消える。
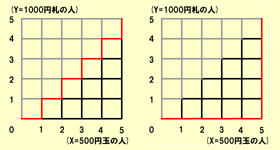
左図の赤い線は、500円玉の人と1000円札の人を交互に受け付けた場合。右の図は、500円玉の5人を優先的に受け付け、その後、1000円札の人を受け付けた場合だ。この図は、どの経路を取っても、つり銭が足りなくなることはない。そこで、各格子点に行く経路の組み合わせ数を考えてみる。
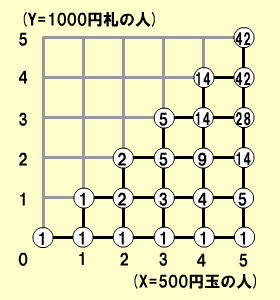
ひたすら、経路を数えてみると、5人+5人=10人の場合は、42通りの組み合わせがあることがわかった。「ん? この表、どこかで見たことがあるぞ!」と思ったら、「カタラン数」だ。
つまり、問題文から、これは「カタラン数」を使えば求めることができることを見抜き、「カタラン数」の公式を知っていれば、答えることができる。または、問題文からカタラン数の公式を導出できる天才だ。この問題は1990年の国際数学オリンピック(IMO)日本代表選抜2次試験に出された問題の類題で、第1次予選の通過者123人中、10人が正解したとのこと。
ちなみに、この問題の解答、カタラン数の公式は、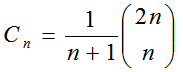
5人・5人の場合で検算してみよう。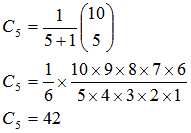
「たけしのコマネチ大学数学科」29講で「カタラン数」の問題が出題されたときは、「カタラン・ワカラン数」だったが、なんとなくだけど、少しわかったような気になった。
 完全攻略 数学オリンピック 著者:秋山 仁,ピーター フランクル |