風呂上りに体を拭いていたら、ギックリ腰になってしまった;; そんな無理な体勢をとっていたわけではないのだけれど、やはり、家から一歩も出ない生活をしていると、筋力が弱っているからなのだろうか。弱り目に祟り目、泣きっ面に蜂の「たけしのコマネチ大学数学科」第72講。今回の演題は「ラッピング」。

問題:1辺が10cmの立方体の箱を1枚の長方形の包装紙で包むとき、できるだけ包装紙を節約したい。その最少面積を求めよ。ただし、立方体のどの部分も覆われていなければダメ、包装紙の裏が見えてもダメ、紙にハサミを入れてもダメよ。
コマ大数学研究会の面々は、川越市にある「丸広百貨店」に。じつは、地元に根付いたダンカン、ちゃっかり広報誌に推薦文を書いていたり、ダンカンの声で店内アナウンスが流れていたりした。そこで販売サービスのプロから包装の手ほどきを受ける。
マス北野は、昔、デパートのアルバイトなどもしていたそうで、包装の技術は、昔取った杵柄で、今でもたいしたもの。プロで難しいと言う、立方体をキレイに包装する。
いつもは、コマ大生からの解答発表だが、今回は、マス北野から……。ボードには、いろいろな数字が書き込まれていたが、12×100なら、1200平方センチで、立方体の表面積の2倍だし、6√2×100でも、約848.5平方センチだ。完全にギブアップの体。
東大生チームの答えは「800平方センチ」。基本の十字形(立方体の5面)+残り1面の正方形を4分割して出来る三角形で覆う作戦だ。以下の図のような包装を考えた(グリーンの部分は、折り込み箇所で、重複する)。
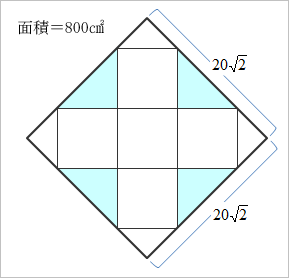
でも、同じ800平方センチの包装紙なら、こんな手の込んだことをしなくても、次のような包装方法でもよい。
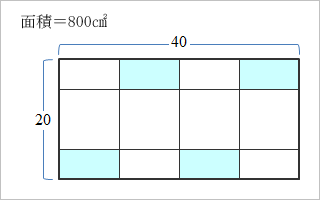
さて、コマ大生だが、ダンカンは、立方体の辺と同じ幅の包装紙で巻くことを考えた。そこでアタルくんがひらめいた、ひさびさのアタルチャンス! 「ならば、包装紙の幅をもっと狭くしてもいいのでは!」包装紙と一緒に、幅1cmのリボンがあるではないか。しかし、実際にリボンを立方体の面にキレイに巻いていくには、重なりが必要で、計算上は「910平方センチ」という答えになった。
マス北野からは、「リボンの幅を狭くすりゃあ、立方体の表面積に近づく、微分だよ」と声がかかる。まさしく、その通りなのだ。
中村亨センセの「美しき数学の時間」でも、今回、正解はなかったものの、考え方としては、コマ大生の発想が正解と言っていた。
まず、普通にラッピングする場合、どれだけ小さい包装紙で包むことが可能かを検証しておこう。
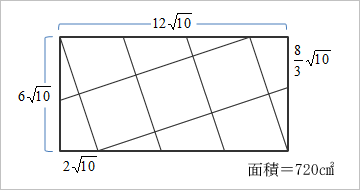
上の方法を、さらに工夫すると、こうなる(図は、いいかげん;;)。
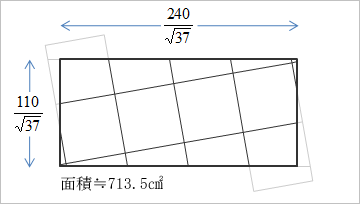
じつは、もうひとつ、紹介されていたのだが、ごめん、よくわからなかった;;
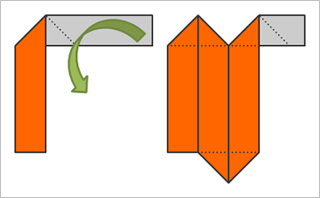
で、発想を転換し、細長いリボンのような包装紙があるとすると、次のような方法で立方体の表面を覆うことができる。
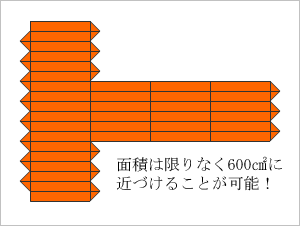
折り返しの三角形の部分は、包装紙の幅を狭くすることで、いくらでも小さくできる。包装紙の最小面積は「600平方センチに限りなく近づけることができる」というのが正解。
コマネチ・フィールズ賞は、ちゃんと面積を出して、きちんと図で証明した中では、最小ということで、東大生チームが獲得したが、マス北野の「長方形にダマされたな」と言うとおり、発想の転換という点では、私だけでなく、番組を見た誰もが、コマ大生に軍配を上げるだろう。「コマ大、ファイト、ファイト、ファイト!」
≪参考≫
■知性の織りなす数学美

コマネチ大学 #71
コマネチ大学 #71
たけしのコマネチ大学数学科#71 2007/12/20 深夜OA
今回のテーマは、
「ラッピング」
【定番本】
コマ大数学科
特別集中講座
ビートたけし
¥1,000
【New】
逆転発想力パズル
脳が目覚める
竹内薫 中村亨
¥1,2…