ジャンボ宝くじの賞金総額は発売額の48.0%なので、300円の宝くじ券の期待値は、144円だ。それでも宝くじに夢を馳せるのは、1等賞金が2億円、2等賞金が1億円と高額なためだろう。宝くじの発行枚数は1000万枚、1等は1枚、2等は5枚なので、1等あるいは2等が当たる確率は「6/10000000」、大丈夫、サイコロを8回振って連続して「1」を出す強運の持ち主なら「たけしのコマネチ大学数学科」第61講。今回は、ちょっと変わったサイコロが登場する。

問題:直方体の各面に1~6まで数字を書き、サイコロのように転がす。ある数の出る確率が1/9で、別のある数の出る確率が1/4、さらに出る目の期待値が「3」のとき、3の反対側に書かれている数字は何か? ただし、向かい合う面に書かれている数の和は7とは限らない。
コマ大数学研究会の面々は、今回も体を張った検証を行うのだが、中村亨センセのヒントを得て、1、2、3、「ダーーーツ!」で勝負。このダーツの的を見て、私は直感的に3秒で答えがわかった^^;だって、期待値がサイコロの「3.5」より低い「3」なのだから、円の1/4の(黄色:90度)部分には、誰が見たって「1」と「2」が入ることは明白。で、円(360度)の1/9は、40度なので、残りは50度ということになる。サイコロの残りの目は、「4と5」、「3と6」に分けると、「4と5」「3と6」の面積の比率に関係なく、円の半分は、ともに期待値は「4.5」、もう半分(1と2の部分)の期待値は「1.5」となる。全体の期待値は「4.5+1.5」の半分で「3」になるでしょ。
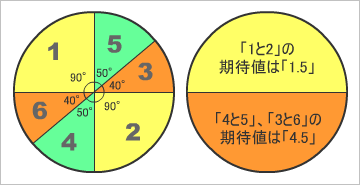
というわけで、コマ大数学研究会は、円グラフ中の数値の場所を変えつつ、ダーツを投げて「平均値」を算出する作戦だったが、これでは、あまりにも効率が悪いので、〆さばアタルが「第15講:ビュフォン」の回で、風呂場のタイルの上に牛乳瓶のフタを一度に「ばぁーっ」と投げる方法を思い出した。今回も、同じ手法を用いる。それは、円形のプラウタンに「カイワレ」の種を一度に蒔く方法だ。その成果をスタジオに持ち込んだときには、カイワレは芽を出し、しっかり育っていた。無法松の「カイワレハウチュウジンダ!」には笑ってしまった。ガダルカナル・タカの「カイワレはカイワレだろ」というツッコミもじつに的確だ。
で、コマ大数学研究会の結論は「3の対面は5」という答えで、実証による平均値は「2.99」になった。マス北野は(a,b)(c,d)(e,f)とペアになる数に(1/9)、(1/4)の確率を掛け合わせた方程式を立て、答えは「6」。東大生チームも、ペアとなる数字の確率は同じということから、期待値が最小となる数の組み合わせを考え、答えは「6」となった。
それでは中村亨センセの「美しき数学の時間」。
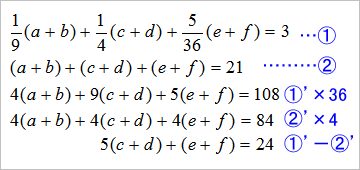
ペアとなる数字と確率を掛け合わせた方程式①は、マス北野と同じ。でも、両者とも気づかなかった、1~6までの数を全部足すと「21」になる式②を立てた。①の式に36を掛けて分母をはらう…①’、4(a+b)を消すために②の式を4倍する…②’
①’の式から②’の式を引くと、5(c+d)+(e+f)=24になる。(c+d)が5以上になると、右辺の24を超えてしまうので、(c+d)は、3か4だ。4を代入すると(e+f)も4になってしまうので、(c+d)は「1と2」に確定する。残りの(a+b)と(e+f)だが、24-5(c+d)=9になり、ふたつの数を足して「9」になる組み合わせは、「4と5」、「3と6」になる。(a+b)、(e+f)のどちらに入っても、その組み合わせは変わらない。
では、検証してみよう。
ルーレットが止まった場所の数を足して、試行回数で割る。Flashの速度的限界があるため、動態視力のいい人なら、目押しができるかも知れないので、確率の検証としては問題があるかもしれない^^;「停止」ボタンを押してから止まるまで、タイムラグを設けようかと思ったが、そこまでする必要もないだろうということで……。「自動」ボタンを押すと、100回のシミュレートを行う。ルーレットの止まった位置ではなく、内部の乱数によって判断している。「自動」にすると、ルーレットの回転も遅くなっちゃうし><;
※追記:確実に狙った場所で止められる;;意味ないじゃん!

コマネチ大学 #60
コマネチ大学 #60
たけしのコマネチ大学数学科#58 2007/09/06 深夜OA
今回のテーマは、
「期待値」
コマ大数学科特別集中講座/ビート たけし
¥1,000
◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇
ある実験を繰り…
いつも楽しく拝見しています。
今回の問題は以下の回答ではまずいでしょうか?
3分くらいで解けたので、気持ちが悪いですね。
各面の数字をa,b,c,d,e,f,gと置くと、期待値3から、
1/4(a+b)+1/9(c+d)+5/36(e+f)=3
↓
9(a+b)+4(c+d)+5(e+f)=108
↓
4(c+d)+5(e+f)=108-9(a+b)
4(c+d)+5(e+f)=9(12-a-b)
両辺が整数であるため、
c+d,e+fは共に9の倍数となるため
c+d=e+f=9
3の対面の数字は9-3=6
どうでしょうか。
こんにちは。N.G. です。
また、確率の問題でしたね。
たかたかさんの解法ですが、c+d,e+fは共に9の倍数であるというのは、式の両辺が整数であるための十分条件ではありますが、必要条件ではありません。たとえば、c+d=e+fが成り立つと左辺は9(c+d)となるので、9の倍数となります。したがって、両辺が整数であることからは、c+d,e+fが共に9の倍数であるということは導き出せないと思います。
ところで、目の出る確率が1/4,1/9,5/36となるようなサイコロってどんな形なんでしょうね。面積比が確率に比例するのであれば、直方体の各辺をx,y,zとして、
x・y=9
y・z=4
z・x=5
を解いて、
x=3・√5/2
y=6/√5
z=2・√5/3
これに6・√5をかけて整数比にすると
x:y:z = 45:36:20
となります。私は物理学をわかっていないのでこれで、目の出る確率が1/4,1/9,5/36になるのかどうかわかりませんが、転がりとかを考えるとこんなに簡単には行かないような気がしています。作って試してみればいいのでしょうが、私にはコマ大生のような気力も体力もありませんです。。。
私が子供の頃、将棋の「金」の駒、4枚(7面体なのですが)を転がして、表がでたら「1点」、裏が出たら「0点」とするだけでなく、駒が立った場合を考慮した得点(重み付け?)で遊んでいたことを思い出しました。言葉で説明するのは難しいのですが、将棋の駒の一番長い辺で立った場合は「5点」、2番目に長い辺で立った場合は「10点」、そして、五角形の上の部分、一番短い辺で立ったときは「15点」とカウントしていたように記憶しています。将棋の駒を投げたとき、確率的に起こりにくいほど、高い点数になるわけですが、投げ方を工夫することで、けっこう高得点を狙えたような気がします。
私がShadeで作成したサイコロの図(もちろん、面積比は、いいかげん^^;)では、角を丸めていますが、これによっても、かなり転がり方がちがうでしょうね。