 算法少女 著者:遠藤 寛子 |
「たけしのコマネチ大学数学科」は4月以降も番組継続が決まり、うれしい限りだが、番組改編時期の特番が入り、このところ休講状態。で、今回は「算法少女」の冒頭に出てくる問題を考えてみよう。「算法少女」は、安永4年(1775年)江戸で出版された和算書と同じ題名だが、遠藤寛子さんの「算法少女」は、その和算書を医者の父「千葉桃三」と共に著した「千葉あき」(当時13歳)の物語(小説)だ。
帯に「江戸時代にも算数好きの女の子がいた!」「和算の世界へいざなうジュニア歴史小説」とあるように、児童文学作家の遠藤寛子さんの小説は、もちろん大人が読んでも文句なしに面白い。
物語は江戸浅草の観音さまに「あき」たちが出かけ、ある「絵馬」を見つけるところから始まる。その「絵馬」には、次のような算額の問題が描いてあった。

「今、半円ノ内ニ、図ノ如キ勾股形(直角三角形)と二円アリ……」半円に内接した直角三角形に内接する円と、弓形内に描いた最大円が、共に等しく4寸であるとき、大円(外接円)の直径を問う問題である。この絵馬を奉納した「三之介」は、この答えとして「1尺2寸」と書いていたのだ。江戸時代、算法の勉強をしている人が、自分の勉強の成果を観音さまに見ていただく、お礼の意味で絵馬を奉納することがあったそうだ。でも、多くの人が目にする絵馬なので、自分はこんなにむずかしい問題も解けるほど算法に長けているという自慢をするために絵馬を奉納する人もいたんだよね。武家の水野三之介は、そんなヤツ。関流の藤田貞資(ふじたさだすけ)の直門の弟子として算額を学んでいた。ところが、町娘の「あき」は、この絵馬を見て「どうもへんだわ」とつぶやいてしまう。
「あき」は、以前、この問題を父から出されていて、解いていた。小円(内接円)が4寸の場合、大円(外接円)の直径は「1尺3寸」になることを……。で、それを耳にした三之介にとっては、大勢の前で自分を否定されたようなもの。とくにこの時代、武道や書道、華道にいろいろな流派があるように、算法にもいろいろな流派があり、互いに自分の流派を誇り、他の流派を貶める傾向があったそうだ。いきなり、ひともんちゃくがある展開で、ぐいぐいと物語に引きこまれていくのだけれど、小説では、その解法までは描かれていない。
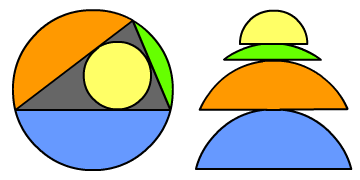
そこで、円に内接する三角形と、さらにその三角形に内接する円の関係を考えてみよう。円に内接する三角形が作る、3つの弓形の高さ(垂直線の長さ)とその三角形に内接する円の半径を足すと外接する円(大円)の直径になる(これも、証明が必要だけど^^;)。まあ、話を進めると、絵馬の問題の場合、半円なので、図のブルー の部分は、外接円の半径になる。つまり、大円の半径は、次のようになるはず。小円(内接円)の半径の3倍、ちょっと。この「ちょっと」が重要で、これを見逃すと、三之介のように、半径2寸の3倍は、6寸。直径はその倍なので、12寸、1尺2寸という誤った答えになってしまう。
で、現代の幾何数学で、どのように解いたらいいのか。インターネットで調べてみると、やはり「算法少女」の問題を解いているサイトがあった。
「算法少女」の水野三之介は何を間違えたか
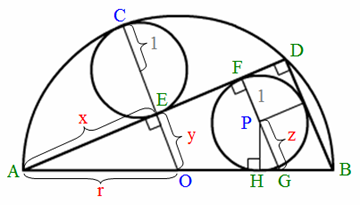
考え方を簡略化するため、小円の半径を「1」としている。
以下、上記サイトのそのままの受け売りだが、△AEOと△AFGの相似性から、x:y=2x-1:z+1、すなわち、(z+1)x=(2x-1)y
次に△AEOと△PHGの相似性より、x:r=1:z、すなわち、z=r/x
この2式よりzを消去して、r+x=(2x-1)y
またOC長はr=y+2なので、y=r-2
yを消去すると、r+x=(2x-1)(r-2)
xを解くと、x=2(r-1)/(2r-5)
ピタゴラスの定理(x^2+y^2=z^2)に適用し……
ええい、めんどうくさい;;詳しくは、上記サイトを見てほしい。
結果的に、r=13/4 になる。
小円の半径は「2寸」直径は「4寸」なので、4倍すると、13寸。
つまり、大円(三角形に外接する円)の直径は1尺3寸となる。
この「算法少女」をおもしろいと感じるのは私だけではないはず。一度は、岩崎書店から「1973年」に発行されるものの、その後、絶版となり入手が困難になった。しかし、さまざまな数学者や、この本の愛読者の支援で「ちくま学芸文庫」で復刻されたように、熱烈な読者がいること。そこは、遠藤寛子さんの「数学を学ぶ本質」を説いているからだと思う。数学は身分などカンケーなく、ましてや流派などにもカンケーなく、ホントのところを知りたいココロだ。わからなかったことを理解したヨロコビだ。ぜひ、江戸時代にいた算数好きな「あき」のその後のエピソードは、この「算法少女」を読んで、それぞれが自分の中に落とし込んでほしいと思う。酔っ払い爺の私なんかが言うのも、おこがましいが「すばらしい」。

不躾とは存じますが突然お便りいたします。
算法少女の問題で、直線COは直線ADの垂直二等分線になっていることがわからないと解けませんが、問題を解く上では自明なこととして処理されます。
円弧ACDと弦ADの中に内接する円の中心の軌跡はOを焦点とする放物線になりますが、西日本のメル友はその計算は高校の授業でやったというのです。
東日本の3人は余り記憶にないので、受験勉強に対する東西の力の入れ方の差だろうかと想像しているのですが、Gascon様の見解を賜りたくコメントいたしました。
愚問で申し訳ありませんが、宜しくお願い致します。
Carbonaroさま、コメントありがとうございます。
私は、高校時代、漫画ばかり描いていて、いつも寝不足の状態で「数学」の授業は、まったく覚えていません^^;放課後になると、やっと眼が覚め、美術室で食パン(木炭デッサンの消しゴムがわり)を食べながら、たむろするといった毎日でした。そんなわけで、私に聞かれても、わかりません。
ただ、高校のカリキュラム(教育課程)の指導方針は地域によって違うというよりも、年代によって、かなり変わっていると思います。また、学校(とくに私立校の場合など)によっても、どの学年でどこまで教えるかが違ってくるようです。いずれにしろ、授業の時限数は限られているので、かなり、駆け足というか、なんとか消化するといった感じにならざるを得ないという話も聞きます。
もし、教育現場にいる先生方がご覧になっていたら、フォローお願いします。
素晴らしい青春時代を送られたようで、驚きました。
赤塚不二夫のコメントがあった理由も分かりました。
愚問にも丁寧に回答いただきありがとうございました。