コマネチ大学数学科38講の「スパゲッティ問題」で、大ポカをやらかした酔っ払い爺の私。コマ大数学研究会と同じく、モンテカルロ法で確認してみようと思った。
問題:1本が30cmのスパゲッティを無作為に3本に折ったとき、その3本で三角形を作ることができる確率は?
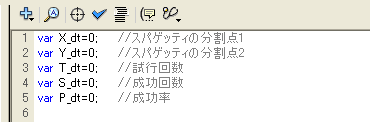
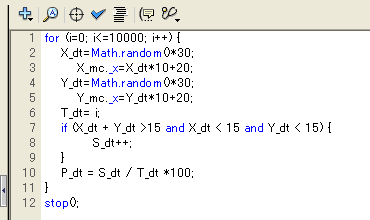
1本のスパゲッティを任意の2箇所で折る。三角形を作ることのできる条件として、三角形の二辺の和は他の一辺より長いので、X+Y>15とした。かつ、X,Yともに一辺が15cmを超えると、他の二辺の和よりも長くなってしまうので、X_dt<15、Y_dt<15 の条件を加えた。これをコマ大数学研究会が試した1000本の10倍、10000本繰り返し、三角形を作ることができた場合をカウントしてみる。正解は「1/4」なので、25%あたりに収束するはず。ところが何度トライしてみても、12.5%あたりに収束してしまう。たぶん、三角形を作ることのできる条件が間違っているのだと思うのだが……。アルコール漬けの脳では、よくわからない。

いつも、こちらのサイトを楽しく見させてもらってます。
(毎回プログラムで解答を見せてもらえるので
すごいなぁと感心しております。)
ところで、
X_dt, Y_dt を左端からの長さで定義してるので、
3つに折ったときの各辺の長さは
X, Y-X, 30-Y ですね。(X, Y, 30-X-Y じゃなくて)
ですから、
全体条件としては、
X>0
Y>X
Y>30
このうち三角形になるのは、2辺の和>他の一辺から
Y>15
X>15
Y<X+15
ですよね。
分割の定義は、3辺を X, Y-X, 30-Y と設定してるのに
対して、下の for 文内の条件は
3辺を X, Y, 30-X-Y で考えた場合で、
計算されてるので、そこで矛盾が生じてるようです。
確認してみてください。
コメント、ありがとうございます。
コメント欄では説明しきれないので、
別エントリーにて、解答します。
■同時確率と条件付き確率
またまた、「コマネチ大学数学科」38講の「スパゲッティ問題」である。茹でる前のスパゲッティを折る話なので、こんがらがることはないと思うのだが、私の頭の中では、複雑にからみついて、なかなか解きほぐせない。 前回の「スパゲッティ問題(その2)」では、モンテカルロ法でこの問題を解こうとしたら、期待したとおりの値にならなかった。変数名や図がひとりよがりでわかりにくく誤解を与えた部分があったので、そのへんを…