世界女子バレー、日本は残念ながらメダルに手が届かず。ロシアとブラジルが世界1位の争いを繰り広げる中、「たけしのコマネチ大学数学科」の第27回。今回のお題は「一筆書き」。下のおダンゴを4つ串刺しにしたような図形のAから描き始め、Bに辿り着く書き順は何通りあるか答えなさいというもの。
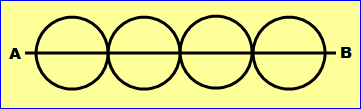
ひとつの円に注目すると、最初の分岐は3通り。で、戻るときは、来た道を引き返せないから「3-1」の2通り。つまり、ひとつの円に対して3×2=6通りの書き順があるわけで、それが4個だと、6^4=1296通り。ここまでは、誰しも納得というか、すぐに計算できる。
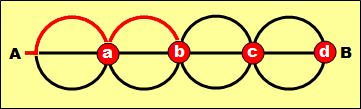
問題は、複数の円にまたがり、たとえば、上の円弧だけを続けて書き、戻る方法だ。しかし、これもよく考えると、連続して書き始めたポイントまで戻るしかないことがわかる。ひとつ目の円はすでに組み込み済みなので「a」は除外される。残りは3つ。戻る手順は2通りなので、2^3=8通り。つまり、(6^4)×(2^3)=1296×8=10368通りが答えとなる。
円がn個つながったときの公式は、
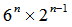
番組では、東大生チームがみごと正解してフィールズ賞を獲得した。
ちなみに、ある図形が一筆書きができるかどうか、有名な「ケーニヒスベルクの橋渡り」については、過去の記事「第8回:トポロジー」を参照してね。

たけしのコマネチ大学数学科 第27回 - 一筆書き
本当は放送の順番通りに解説回答していこうと思っていたのですが、どうも、今週放送に