ガスコン研究所BLOG

　私は「数学」の落ちこぼれだ。こんなカミングアウトをしたところで、誰もよろこばないのはわかっている。このブログでは「たけしのコマネチ大学数学科」で出された問題を「エクセル」で解いているので、もしかしたら、私を「数学ができる人」と勘違いする方もいるのではないかと思ったからだ。

　私は、2桁の足し算でも電卓を使ってしまうほど、計算がニガ手だ。「春分」や「節分」は知っているが、「微分積分」なんて全然わからない。そもそも、学校で教えてもらった体験がないのだ。私の通った高校は、いわゆる進学校で、成績や目標とする受験大学によって、2年生から、理数系、文系、そして、成績優秀な生徒を集めた文理系のクラスに分けられていた。

  　高校時代、私は漫画ばかり描いていたから、成績は最低。将来は漫画家になるつもりだったので受験勉強もまったくやらなかった。現在の教科書がどうなっているかは知らないが、当時、文理系や理数系クラスの数学の教科書は「数Ⅲ」、文系クラスは「数Ⅱｂ」だった。当然、私は文系クラスだ。「微分積分」は、「数Ⅱｂ」の後半部分にやっと出てくるんだよね。授業がそこまで進んでいないと、教えてもらえないまま、卒業しちゃうのだ（まぁ、当時教えてもらっていたとしても理解できたかどうかは疑問だが……）。でも、教えてもらったという体験がまったくないのとは違うと思う。

　高校卒業後、私は漫画家のアシスタントになり、漫画家として独立し、少年誌で連載をして……そして突然、パソコンに出会う。パソコンに夢中になった私は、某アスキーの面接を受け、デザイナーとしてもぐり込み、その後、編集者になった。

　だから、微分の「lim」なんたらと書かれた数式や、積分の、あの「ｆ」の横棒を取ってデカくしたような（見方によっては音楽のト音記号の渦巻きを取ったようにも見える）記号は、この歳になるまで、まったく知らなかったんだよね。ちなみに、積分の記号は「和 Sum または Summation」の「S」をもじったものらしい。

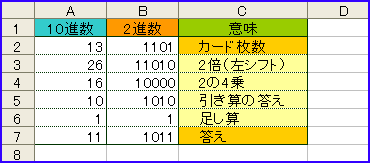
　私の転石の人生は、まだ続き、某アスキーを辞め、フリーのライターになった。あれほど嫌いだった「エクセル」の記事をパソコン誌で書くようになり、仕方がないので「エクセル」の勉強を始め、「エクセル」で使える関数が多くあることを知った。関数の中には難しいものもあって、いったいどんな場面で使えるのだろうかと思うものも少なくない。たとえば10進数を2進数に変換する「DEC2BIN」なども、そのひとつだ。もしも「たけしのコマネチ大学数学科」という番組がなかったら、一生使わなかったかもしれない。

　「たけしのコマネチ大学数学科」の第7回目。今回の問題は、ゲーム「三山くずし」の必勝法を考えなさいというもの。

　問題：「3個、5個、7個の石がある。交互に石を取っていき、最後の石を取ったほうが勝ち。石はいくつ取ってかまわないが、違う山（色）の石を同時に取ることはできない。このゲームの必勝法を考えなさい」

　例によって「エクセル」で表を作ってみる。A列は「=DEC2BIN(C2)」として、C列に入力された石の数を参照して、二進数に変換している。B列の石の山は「=REPT("●",C2)」で、石の数ぶんの「●」を表示している。

　ここまで作成すると、やはり、対戦してみたくなる。しかし「エクセル」でインタラクティブなものを作ろうとすると、どうしても「VBA」を使わざるをえない。「VBA」とは「Visual Basic for Applications」の略で、マイクロソフトの「Office」製品で処理を自動実行させるためのプログラム言語だ。今回の問題は「VBA」の入門として、ちょうどいいかもしれない。

　さっそく「表示」メニューの「ツールバー」から「コントロールツールボックス」をクリックし、ボタンをひとつ作成。このボタンが押されたときの処理を「VBA」で記述する。第6回の二進数の説明のとき「エクセル」では、論理演算子はビット演算ができないと書いたが、「VBA」を使えば、話は別だ。「Xor」（排他的論理和）も使うことができる。

　（※クリックで拡大）

　これで、石の数を減らし「決定」ボタンを押すと、「エクセル」の番になり、石を取る。何も考えていない「エクセル」に必勝法を教えるということは、同時に自分自身がこの問題の「必勝法」に対する理解を深め、より短い記述で整理することにつながる。その結果、先手必勝だが、途中で一度でもミスをすると負けてしまうことになる(^^;。必勝法は、番組を見た方なら、すでにご存知のはず。

　少し、時間に余裕ができたので、前回の「たけしのコマネチ大学数学科」で出題された「ヨセフスの問題」を復習してみたいと思う。

問題「200枚のカードが1から順に並んでいます。1番上のカードを1番下に持っていき、次のカードを捨てるという作業を繰り返したとき、最後に残るカードは何番か答えなさい」

　番組内では200枚のカードだったが、簡略化して13枚のカードで試してみよう。1枚おきにカードを捨てていくので、2周目に入るとき、奇数枚なので、数え始めた「1」のカード（トップ）は捨てられる。残りカードは7枚なので、3周目でもがトップが入れ替わる。残り枚数は4枚なので、トップの入れ替わりは起こらず、「11」枚目が最後に残るカードとなる。

　これを数式にすると、カードが偶数の場合は(2n)枚、奇数の場合は(2n+1)枚のカードがある。1周した時点で残るカードの枚数は、偶数の場合(2n/2＾2)、奇数の場合は(2n/2＾2)+1になる。3周時は（2n/2^3)……と続き、最終的に（2n/2^s+1)+1となるはずで、f(n)=2(n-2^s)+1という式になる。

　ここでの「ｓ」とは、何周したかであり、つまり2の何乗かであるかだ。

　番組内でも、カードが200枚の場合、それを2進数で表し、「1」のところは「0」、「0」のところは「1」として、その数を引くと、最終的に残るカードを求めることができると解説していた。

　で、いきなり説明もなく、結論だけを「nを2進数で表し、頭の1を取り、最後尾に付け加える」としたわけだが、これは、ビット演算という手法。10進数を「DEC2BIN」関数で2進数に変換し、先ほどの「2(n-2^s)+1」の式にあてはめてみる。

　「2n」は、2進数の場合、左シフト、ローテーションを行うと、その数を2倍したことになる。たとえば、13の2進数である「1101」を左にひとつずらすと、「11010」になり、それを10進数で表すと「26」。それから「2(2^3)」を引くということは、「2^4」だから、二進数では「10000」、十進数では「16」を引いて、「1」を加えると、答えは、2進数表記で「1011」、十進数表記では「11」となるわけだ（コンピュータの内部では、こんなふうに2進数のビット演算で計算が行われているんですね）。

　このブログは「たけしのコマネチ大学数学科」で出題された問題を「エクセル」で解くことを目的としているが、私を含め、数学にあまり縁のない人にも、とりあえず、難しく考えず「エクセル」を使えば、答えが出せるよ……というのが趣旨だったはず。

　ビット演算なんて、普通の生活の中では、使いません……というか「エクセル」では、10進数を2進数に変換することはできても、AND OR NOT などの論理演算子は、「真：TRUE」か「偽：FALSE」を返すだけで、ビット演算をすることができません。ましてや、左シフト命令なんてありません。そこで文字列操作で「=RIGHT(B2,LEN(B2)-1)&LEFT(B2,1)」とし、左の1文字を取って、右の末尾に加えています。

　今後は、わかりにくい「美しさ」よりも「たけし軍団：数学研究会」のメンバーになったつもりでがんばります。今回、唯一、正解を出したのは、じつは「数学研究会」ですもの。難しい理屈なんて、わからなくても、楽しければいいんだ……。

　木曜深夜は、ちゃんと、お風呂に入り、身を清めて「たけしのコマネチ大学数学科」に望むつもりでいたのですが、風呂上りに「いいちこ（麦焼酎）」を飲んでいたら、番組が終わる頃には、すっかり、出来上がっていました。

　さて、今回のテーマは「ヨセフスの問題」ということで「200枚のカードが1から順に並んでいます。1番上のカードを1番下に持っていき、次のカードを捨てるという作業を繰り返したとき、最後に残るカードは何番か答えなさい」というもの。

　じつは、今回の問題は、以下のサイトをカンニングしてしまいました。

「数学の部屋：『まま子立て（ヨセフスの問題）』」

というわけで、番組を見た方なら、答えはわかっているわけで、なんの説明もない、答えを提示しても、無意味なのですが、酔いも限界なので、このへんで……。

——————-
《追記》

　目が覚めて、「いかん！ 書きかけのブログの記事をアップせねば！」とあせったのですが……。ブログを見ると、ちゃんと載っている……記事をアップしたことさえ、忘れるほど、酔っていたみたい。しかも、答えが間違ってました。申し訳ない。

　解説は「数学の部屋」を見てもらえれば、詳しい説明が載っているので、そちらを見てください。

　ひとつだけ、フォローしておくと、ここで使用している「DEC2BIN」や「BIN2DEC」の関数は、アドインの「分析ツール」を組み込んでいないと「エラー」になってしまいます。この他にも、便利な関数が追加されますので、ぜひ、組み込んでおいてください。

　また「これは、手動で^^;」とありますが、セルB5に「=RIGHT(B2,LEN(B2)-1)&LEFT(B2,1)」と入力すれば、手動で入力しなくて済みます（というか、式を入力するほうが手間がかかる……）。

　「たけしのコマネチ大学数学科」の第5回のテーマは「ケプラー予想」だ。「ケプラー」と言えば「天体運動」が、まず頭に浮かぶが、今回の「ケプラー予想」とは「同一の大きさの球を箱に詰めるとき、一番効率的な詰め方は何か」というもの。いわゆるパッケージ（最密度充填）問題は、証明が難しいらしい。数百年もの間、数学者の頭を悩ませてきたという。

　竹内薫センセの解説によると「ケプラー予想」はヘールズという人がコンピュータを使い、1998年に証明したが、その検証には、やはりコンピュータを使い、2003年に「どうやら99％は正しい」ことが判明したが、いまだ余地が残されているらしい。これが「ケプラー原理」ではなく、「ケプラー予想」と言われる所以だとか。

　さて、今回は「直径5cmの缶は、縦10cm、横502.5cmの枠に何本入る？」という問題。

　縦が10cmなので、2列にして並べれば200本入ることになる。しかし、どうやら「500cm」ではなく、「502.5cm」と中途半端なところがポイントらしい。

　そこで缶の並べ方のパターンを考えてみると、3本を三角形に並べ、それを上下反転しながら並べていく方法が見えてくる。この並べ方で「Xの長さ」が5cmよりも短ければ、それだけ密度が高く、効率的にパッケージすることができることになる。

　まず、缶を3つ並べたときの中心を結ぶ赤い正三角形のを2等分した直角三角形の辺の長さは「2：1：√3」だから、赤い正三角形の高さは「5×√3÷2」になる。枠の縦は10cmなので「10-((5×√3÷2)＋5）」が、枠との隙間、すなわち、青い三角形の高さになるわけだ。

　青い三角形の高さがわかれば、ピタゴラスの定理で、Xの長さを求めることができる。

（※クリックで拡大表示）

　「エクセル」で計算してみると、こんな感じだ。「5+2x」という6缶パックが502.5cmの枠には33個……ということは、33×6で198本入り、余りが10cm以上あるので、1.5×2で3本、つまり201本入るわけだ。

　ううむ、計算上は確かにそうだが、なんかだまされている気がする。本当に201本入るのか。「たけし軍団」と同じく体を張って「エクセル」のA列に1本づつ缶を並べていく（もちろん、オートフィルで連続入力）。ここでは、下段の缶だけを考えることにする。すると、100本入れた時点「=SUM(A1:A100）」で「497.025cm」、101本入れたとき「=SUM(A1:A101）」では「502.025cm」になった。上段の缶は、初めに2.5cmの隙間があるので、100本までしか入らない。美しい方法とは言えないが、これでやっと納得できた。

　私としては、正解を出した「軍団」にもトロフィーをあげたい気分。「たけし」は文句なく正解。女子東大生は、並べ方のパターンに気をとられ、時間切れの「ギブアップ」となった。第5回を終えた時点で「たけし」は2勝2敗1引き分け、女子東大生と並んだ。

　昨日の「たけしのコマネチ大学数学科」のテーマは「折り紙で最大の正六角形を作る」だったので、エクセルの出番はなかった。そこで、番組とは関係なく、正六角形に関連する問題を解いてみよう（ちょっと強引な展開だが……）。補習のテーマは「ルドルフ数」だ。

　古代ギリシャの数学者「アルキメデス」は円に内外接する正96角形を手計算し、少数以下2位までの精度で円周率を導き出した。中世ドイツの「ルドルフ・ファン・コレイン」は生涯をかけて円周率を70桁まで計算したが、正しい値は35桁までだった。ドイツでは、彼の功績を称え、円周率を「ルドルフ数」と呼んでいる。

　円周率を使った計算をするために「エクセル」には「PI」関数が組み込まれている。セルに「=PI()」と入力すれば、小数以下14位までの円周率の近似値を求めることができるが、過去の数学者と同じ手法を用いて「エクセル」で円周率を計算してみよう。計算と言っても、計算は「エクセル」が行ってくれるので、数式をオートフィルで連続入力するだけだ。

　まず、直径１の円に内接する正六角形の辺の長さは、半径が「1/2」なので「6×1/2＝3」になる。外接する正六角形の辺の長さは、ひとつの三角形の高さが「1/2」となり、「6×√3÷3＝2√3」になる。つまり円周率は「SQRT(3)*2」より小さく、「3」よりも大きい。次に辺の数を倍にして、直径１の円に外接する正12角形の辺の長さは、セルを参照して「=(A3*B3*2)/(A3+B3)」、内接する正12角形の辺の長さは「=SQRT(A4*B3)」と入力する。

（※画面をクリックして、拡大表示してね）

　数式を入力したら、あとは簡単。「セルA4」と「セルB4」を範囲選択し、オートフィルで適当な行まで連続入力すればいい。「エクセル」の計算精度の限界はあるが、例では、22行まで入力すると、円周率の小数点以下10位まで正しい値に収束させることができた。

　円周率にまつわる話は多くあり、また、円周率を導き出す式もたくさんある。興味のある方は「円周率ものがたり」や、「πの部屋！」を訪れてみよう。

　2002年、東京大学「金田研究室」が HITACHI SR8000 を用いて「高野喜久雄」の公式と分割有理数化法により 1兆2411億桁まで計算した。

【訃報：2006年5月1日】
　高野喜久雄氏は、詩人として高名な方だが、数学の分野でも、逆三角関数（arctan）を利用した円周率の公式を80年代に発表し、これが円周率計算の世界記録樹立につながった。訃報に接し、心よりご冥福をお祈りいたします。

　このブログは、木曜深夜の数学バラエティ番組「たけしのコマネチ大学数学科」で出された問題を「エクセル」で解くことを目的としているが、今回のテーマは「折り紙でいちばん大きな正六角形を作る」というもの。さすがに「エクセル」では折り紙はできない。第4回目にして、はやくもギブアップである。

　番組を見逃した人のため、折り紙でいちばん大きな正六角形を作る方法を紹介しておこう（これでは、たんに番組を追従するだけだが……）。

　まず、折り紙でいちばん大きな正三角形を作る方法だが、角Ａを中心線に重なるように折る。同様に角Ｂも折る。こうしてできた、「ａ」と「ｂ」を結ぶ線で折ると、いちばん大きな正三角形になる。

　これを踏まえ、正六角形の場合は、折り紙を4つ折にした状態で正三角形を作ったならば、一度、折り紙を開き、対角線ＡＢで折り、先ほど作成した正三角形の折り目を複製する方法で作ることができる。

　ところで、今回の講師は、中村亨（あきら）センセだ。今後は、竹内薫センセと交代で講師を務めるらしい。番組内で印象的だったのは、折り紙で図形を作ることは、コンパスと定規で図形を描くのと同じ。また、コンパスと定規で作ることのできる図形は、２次方程式を解くのと同じだが、折り紙は３次方程式まで解くことができるらしい。コンパスと定規では、正七角形や、正13角形を描くことはできないが、折り紙では可能とのこと。なんか、すごいぞ「折り紙」。

　先週は特番のため、１回お休みとなった木曜深夜の数学バラエティ「たけしのコマネチ大学数学科」。今回のテーマは「モーペルテュイの原理」。私もぜんぜん聞いたことがなく、なにやら難しそうだが、竹内薫センセの解説によると、これは「最小作用の原理」とも言い、要は「自然はムダがなく最小の作用で働く運動を選ぶ」ということらしい。

　そこで、今回の問題はビリヤード。「XY座標（3,3）にある球を3クッションして右下のポケット（座標12,0）に最短距離で入れるためには、どこを狙えばよいのか」という問題。

　右下のポケットに球が入るには、3クッション目が上辺か左辺に当たることになる。番組内でも解説されているので、詳しい説明を省くが、3クッションで右下のポケットに球が入るコースは、3つある。しかし、最短距離ということを考えると、ビリヤード台の短辺でクッションする方法は、除外していいだろう（当然、軌跡が長くなるので……）。

　そうなると、おのずと、コースは見えてくる。問題は、どのポイントを狙うかだ。番組内では、触れられていなかったが、球の大きさは、この際、考慮しない。球に回転をつけて入射角と反射角を変化させるなどという小細工もなしだ。

　で、このブログの趣旨は、問題を「エクセル」で解くことを主眼にしているので、番組とは、違ったアプローチをしてみたいと思う。

　入射角＝反射角なので、グラフ上での傾き（係数）は一定だ。もちろん、反射により、その正負は反転するが……。となると、最初に狙うポイント（第1クッション）を定めたら、第2、第3クッションのX座標は、簡単に求めることができる。

　たとえば、最初にXY座標（4,6）に狙いを定めた場合、Xの増分は1、第2クッションまでは、その倍の距離を進むので、X座標は6となる。第3クッションも増分は2で8、そして、最終的に右下の座標は10になり、ポケットには球が入らないことになる。

　ちなみに、第2クッションのX座標は「=(B3-B2)*2+B3」、第3クッションのX座標は「=B4+B4-B3」、最終値は「=B5+B4-B3」の数式が入る。掛け算と足し算、引き算しか使っていない。

　そして、ここからが「エクセル」の真髄。最終値のX座標（セルB6）を選択した状態で、「ツール」メニューの「ゴールシーク」をクリック。「ゴールシーク」とは、数式を逆算して、結果から元の値を収束させる機能だ。目標値を右下のポケット（X座標「12」）と入力し、変化させるセルには、第1クッションのX座標である「B3」を指定し、「OK」ボタンをクリックする。

　最初に狙う場所は「X：4.285714、Y：6」という結果になった。

　番組では「たけし軍団」はいつものように体を張り「ゴムぱっちん」で最短時間になるような、それぞれのクッション位置を求めたが、ゴムは長く伸ばせば、それだけ縮む速度も速い。ビリヤードの球は転がり抵抗や、反射するときのエネルギーロスを考慮しなければ、等速運動なので、違った結果となる。「たけし」は、最短距離＝直線に目をつけ、立体的なグラフを展開する手法で、ほぼ正解。現役の女子東大生は、三角形の相似を用い、XY座標軸「30/7,6」を導き出した。というわけで、今回の勝負は、引き分け。

　「たけしのコマネチ大学数学科」は、30分番組なのだが、今回は竹内薫センセの解説部分が編集されていて、すべてを聴くことができなかったのが残念……。

　木曜深夜にフジテレビ系列の「数学バラエティ番組」としてスタートした「たけしのコマネチ大学数学科」。第2回の問題は「10分間のファッションショーで水着モデルが登場するのは1分間。しかも、ショーのどこで登場するかはわからない。カメラマンが会場に入ることのできる時間（撮影時間）も1分間。はたして、カメラマンが水着モデルを撮影できる確率は？」というもの。

　今回のテーマは「モンテカルロ法」なので、実際に「エクセル」で確かめてみよう。水着モデルが登場する時間は、0分から9分までの間（1分のショーが義務付けられているから最後の1分間は考えなくてもよい）となる。これはカメラマンが会場に入る時間にも言える。そして、モデルとカメラマンが同じ会場で出会うためには、ふたりの登場、入場時間の差が1分以内であればよい。

「エクセル」の関数で表すと、「水着モデル」の列には「=RAND()*9」、「カメラマン」の列にも「=RAND()*9」と入力。
RAND()：0以上1未満の乱数を返す。引数はなし。
「判定」の列には「=ABS(A4-B4)」と入力。
ABS(数値）：数値の絶対値を返す。（※相対的な差を表す）
セルの条件付き書式で「セルの値が」「次の値より小さい」「1」として
セルのパターンを設定すると、条件に一致したセルが色分けされる。
「試みた回数」（セルC2）には「=COUNT(C4:C103)」とする。
COUNT(範囲）：範囲内のデータ個数を返す。
「撮影できた回数」（セルC1）には「=COUNTIF(C4:C103,"<1")」となる。
COUNTIF(範囲,条件）：範囲内の条件に一致するデータ個数を返す。

　ここでは、番組内で「軍団」が実際に検証した回数、100回を行う。オートフィルを使っても、100行分のデータを入力するのは大変なので、次の方法を試して欲しい。

1:「セルA4」をクリック。
2:「F5」キーを押す。
3:ジャンプ画面が開くので「参照先」に「B103」と入力。
4:「Shift」キーを押しながら「OK」ボタンをクリック。
5:そのままの状態で「=RAND()*9」と入力。
6:「Ctrl」キーを押しながら「Enter」キーを押して、入力を確定する。

　どうです？　水着モデルとカメラマンの100行分のデータが入力されたでしょ。「判定」の列も同じ方法で「=ABS(A4-B4)」を一括入力する。この方法なら、試行回数を「1万回」に設定しても大丈夫だ。

　結果は「たけし軍団」の答えと奇しくも同じ「23/100」となった。もちろん、「F9」キーを押して再計算をすれば、乱数は毎回違うので、結果は微妙に前後する。もっと試行回数を多くすれば次第と正解に収斂していくと考えられる。「たけし」の答えは「19％」。モデルが9分以降に登場することは考えなくてもよいことを見逃したようだ。非常に惜しい。正解は女子東大生の「17/81」。不等式「0＜｜x-y｜＜1」からグラフを用いて、モデルとカメラマンが重なる領域が撮影可能な確率と考え、計算により「17/81」を導き出した。