■コマ大数学科194講：和算Part4

息子から「電子たばこ」をプレゼントされたが、いまだに「たばこ特別税」で旧国鉄の負債を払い続けている爺……「たけしのコマ大数学科」

問題：半径がRの円Oに弦ADをとり、円Oの円周上にA,B,N,C,Dをこの順にとる（Nは弧ADの中点）。さらに弦ADの中点Mに対して、線分MB,MCによって、この円弧を3等分し、それぞれの部分に半径rの3つの内接円を作る。AD=10,MN=4としたときのrを求めなさい。

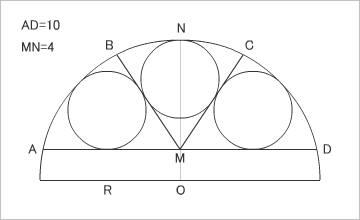
という問題なのだが、どーやら問題文に間違いがあるようだ＞＜；

爺は、Flashのスクリプトを使い、問題図を作成した。弧ADを三等分すると、真ん中の小さな円が苦しいのが、わかってもらえると思う。等しい直径の円が3つ入らないのだ；；

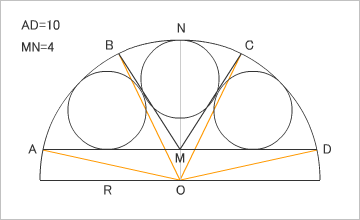
もちろん、∠AMD（180度）を三等分して、60度ずつ分割するのも間違いだ。爺の「いいちこ」な塩梅による計算だと、∠AMBは、弧度で「0.981765356578622」、角度に直すと「56.2510114041114」となった＾＾；

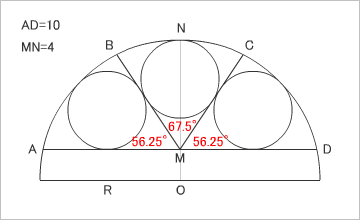
問題文の「弧ADを三等分」というのは、間違いだが、今回の問題を幾何的に解く場合、具体的な角度は、必ずしも重要ではない。大円の弦ADをどこにとるかで、この角度は違ってくる。重要なのは、大円を切り取る弦と弧の内側に等しい直径（半径）の小円が3つ収まる状態のとき、小円の半径を求めること。

前置きが長くなってしまったけれど、コマ大数学研究会は、最初から神だのみ。「アクアシティお台場神社」にお参りしたあと、しめ縄を使い、地面に描かれた大きな問題図で検証。

●コマ大数学研究会の答え「1.35」

マス北野は、いつものように、コンパスと定規で、できるだけ正確な図を描いていく。どうやら、コンパスで測ると1.5くらいになるという目星をつけたが、補助線を何本引いても、うまい解法が見つからないままタイムアウト。

●マス北野＆ポヌさんの答え「1.ζ」
※1.3とも、1.5とも読めるような答えを書いた＾＾；

小橋りささん＆岡本麻希さんの東大生チームは、直角三角形の相似比と三平方の定理を使い、なんとか小円の半径を求めようとゴリゴリ計算したが、あらかじめ立てた戦略の筋書き通りに行かず、答えが出せない。

●小橋りささん＆岡本麻希さんの答え「1.5くらい？」
※数学の問題の答えに「くらい」、しかも「？」までついているので、みんなから非難轟々＾＾；

正解：小円の半径は「10/7」。小数に表すと、約1.42857……どのチームも、自分のチームの答えが近いと、騒然となったが、今回は、コマ大フィールズ賞はなし。

●竹内薫センセの「美しき数学の時間」

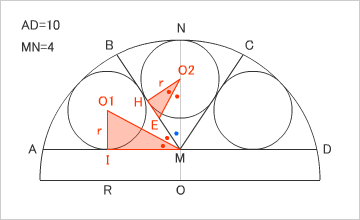
戦略としては、直角三角形「O1MI」と「O2EH」が相似であることを証明し、相似比を使い、小円の半径「r」を求める。

今回の問題はややこしいので、ひとつひとつステップを踏んでいこう。まず、相似であることの証明。Eは、∠HO2Mを二等分する、線分BM上にとった点である。∠AMNは直角。∠O1IM、∠O2HMも直角。三角形の内角の和は180度なので、∠BMN（図の青い点）を直角から取り除いた角度を二等分した角度が、∠O1MI、∠HO2Eになる。ゆえに、∠O1MIと∠EO2Hは等しい。直角三角形「O1MI」と「O2EH」はすべての角が等しいので、相似形である。

すると、相似比で「r：IM＝HE：r」が成り立つ（rは、小円の半径）。

・大円の半径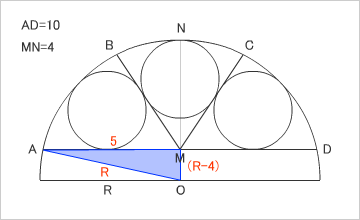

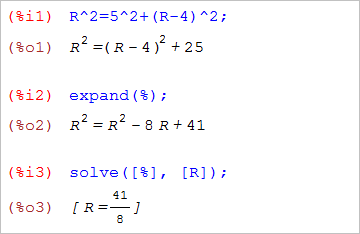
まず、Oを中心とした大円の半径を求めておく。三平方の定理を使えば、R=(41/8)と求まる。

・IMの長さ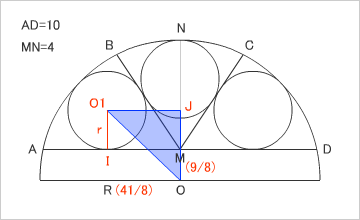

IMの長さは、O1Jの長さと等しい。O1Jの長さを求めれば、IMの長さになる。JOの長さは、小円O1の半径(r)とMOの長さを足したもの。O1Oの長さは、大円の半径(R)から小円の半径(r)を引いたものだ。三平方の定理で、IMの長さを求めることができる。

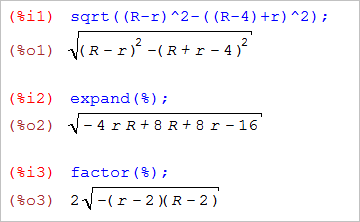
・HEの長さ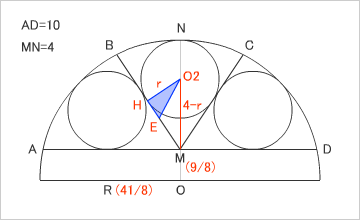

Hは、小円O2と接線BMの接点。∠O2HMは直角。O2Hは小円の半径(r)、O2Mは(4-r)なので、HMの長さは三平方の定理で求まる。で、HEの長さは、角の二等分線の公式(HE:EM=r:4-r)を使い、計算する。

・小円の半径(r)を求める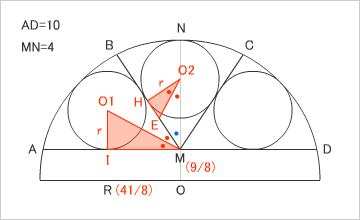

さあ、これで計算に必要なものは揃った。ふたつの直角三角形の相似比を使い、小円の半径(r)を求める。

番組内では、細かな計算過程は省略されたが、とにかく爺は、Maximaのおかげで、なんとか小円の半径を求めることができた。しかし、たった10分間でこれを手計算しろというほうが酷という気もする。

もっと、簡単な解法はないのだろうか……。というわけで、今回のテーマ「和算」の話になる。

※引用：「続算学小筌」(1832年：牛島盛庸(うしじま・もりつね)）

おせっかいを承知で「いいちこ」な爺が、わかりやすい現代的な表現にしてみた＾＾；

図のように斜めに隔てた（区切った）弧の内に、3つの等しい直径の小円を容れる。弦の長さは「四寸」、矢の長さは「一寸」のとき、等しい小円の直径を答えよ。
答え、等しい小円の直径は「八分」。
解法は、弦と矢を乗算した値を、弦と矢を足した値で除算する。これで等しい小円の直径を得ることができる。

（※どこにも、円弧を三等分するなんて書いてない）

つまり、弦(4)×矢(1)÷(弦(4)＋矢(1))＝4÷5＝0.8
円の直径は「8分」となる。

今回の問題に適用すると、弦(AD=10)、矢(MN=4)なので、(10×4)÷(10+4)＝40/14＝20/7　これは、直径なので、半径はその半分、10/7となる。「続算学小筌」の問題と、今回の問題とは、弦AD、矢MNの長さも違うのに、この解法で答えを求めることができるということは、天保3年に書かれた「続算学小筌」の正しさを現在の数学で証明したことになる＾＾；

しかし、天保3年の江戸時代の人が、どのような解法で、この答えにたどり着いたのだろうか（江戸時代には、Maximaやパソコンなんてものはなかっただろうし＾＾；）。

番組内で竹内センセは、「2ab/(a+b)」というのは、調和平均を求める公式なので、もっと簡単な解法があるかもしれないと言っていた。

そのヒントとなるのが、「算法新書」(1830年：千葉胤秀(ちば・たねひで))だ。

※引用：「算法新書」(1830年：千葉胤秀(ちば・たねひで))

「半梯」というのは、等脚台形を垂直に二等分した台形のことのようだ。直角がふたつある。

「算法新書」には、このような図解が載っているのだが、問題の寸法と図の寸法がかけ離れているし、わかりにくいので、説明用のFlashを作成した。

※Playボタンを押してほしい。

「半梯」の下底をa、上底をbとすると、円の直径は、「2ab/(a+b)」という式で求められることがわかった。

このヒントを今回の問題に適用してみる。

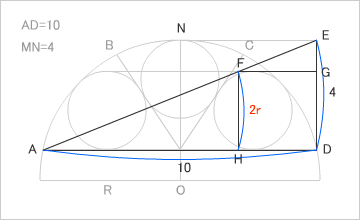
Dを通る垂直線を引く。Nを通り、ADに平行な線分を引く。その交点をEとする。AとEを結ぶ線を引く。ふたつの小円に接するような、ADに平行な線を引く。AEとの交点をF、EDとのこの交点をGとする。また、FからADに垂線を引き、交点をHとする。「算法新書」では、FGとFHは、円の半径だったので、FG＝FH、この問題の場合は、FGとFHは、ともに円の直径、つまり、□FGDHは、正方形。△EFGと△EADは相似。ここまでくれば、「算法新書」の方法で、円の直径を求めることができる。「算法新書」と違うところは、円の半径ではなく直径だというところ。だから、倍することなく、「ab/(a+b)」という「続算学小筌」の答えになる。

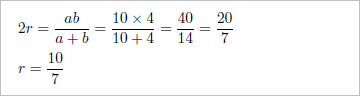
コマ大数学科の問題は、小円の半径を求めることなので、2で割る。

ところで、今回のちょっといい話は、いろいろな「平均」の話だった。

ふつー「平均」と言ったら、足して2で割るよね。これを「相加平均」または「算術平均(Arithmetic mean)」と言う。企業（売上）の成長率などの平均は、「相乗平均」で予測することができる。「相乗平均」は「幾何平均(Geometric mean)」とも言う。で、「調和平均(Harmonic mean)」は、ハーモニックとあるように、ピタゴラス音階と関係がある。株式証券をできるだけ安く購入する方法として「ドル・コスト法」があるが、これにも「調和平均」が関係している。まぁ、世の中、いろんな平均に満ちているわけだが＾＾；

今回、爺がすごく驚いたのは、「円」と「平均」の関係だ。「円」と言っても「お金」のことではない＾＾； ミステリーな「円」だ。「和算」というと、どこか、門外不出の秘術めいていて、その解法について触れていないことがあるけれど、江戸時代後期になると、いろいろな公式集みたいなものも、出回っていたみたい。「和算」の問題には、「円」の性質を使ったものが多いように、爺は感じる。それほど「円」は、ミステリーなのら＾＾；

上のFlashは、円の直径を「10」としたとき、直径上の任意の点を「G」とする。AG=a、BG=bなので、(a+b)/2=半径となる。あたりまえちゃ、あたりまえだけど、これが「相加平均」。いわゆるふつーの「平均」だ。「G」を通る垂線を引き、円弧との交点を「P」とすると、PGは「相乗平均」になる。さらに、「P」と円の中心「O」を結び、「G」から線分「PO」に対して垂線を引き、交点を「H」とする。この「PH」が「a」と「b」の「調和平均」になるのだ。

そんなうまい話が……というわけで、疑がり深い爺は、それぞれの「平均の公式」で計算した結果と、Flashの「Point」という機能を使い、それぞれの点の距離を求めて検証した＾＾；

近似値計算の誤差が表れることがあるけれど、どーやらホントみたいだ。

それにしても、「和算」に目覚めた、江戸時代の人は、こーいった「円」や「直角三角形」の持つ性質の不思議さに気付いていたんだろうな……。

酔っ払い爺の妄想だが、もし、爺が「創世記」を書くならば、「神は、はじめに真円を描いた。『ま、そーゆーことだから、あとは、よろしくね！』と神は言い残し、どこかに去ってしまった……」と書くかも＾＾；

≪参考≫
●東北大学 和算資料データベース

・「続算学小筌」の該当頁

・「算法新書」の該当頁

※追記（補足）2010年9月17日

ちょっと言葉足らずで、わかりずらい部分もあったと思うので、もう少し説明を補足する。

今回の問題は、問題図から答えを出そうとすると、なかなか埒があかない。そこで「算法新書」のヒントを得て、上底(4㎝）と下底（10㎝）の端が左右どちらかに揃っている台形に半径(2r)の円が内接するとき、この台形の高さを求めれば、結果的に小円の直径(2r)も求まると爺は考えた。補助線というより、問題をすり替えちゃうのね＾＾；

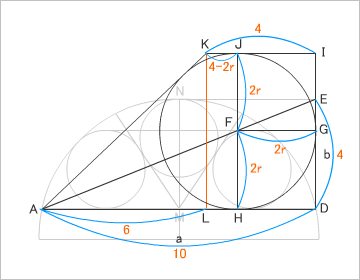
「算法新書」では、今回の問題の矢の長さ(NM)が台形の上底（KI：4cm）と等しいことを証明している（※説明用Flash参照）。NM=ED=4。この台形に円が内接していると考えると、FHとFGは、ともに内接円の半径なので、FH=FGとなる。FHは小円の直径。つまり、この台形の高さ＝内接円の直径は、小円の直径の2倍になる。

「算法新書」の解法（※爺の推測による、勝手な解釈を含む）
△ADEと△EFGは相似形なので、EG：ED＝FG：ADが成り立つ。

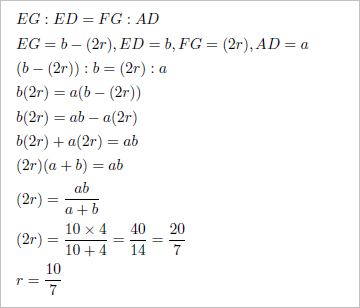
「算法新書」では、小円の直径＝（上底×下底）÷（上底＋下底）という、答えを導き出したが、「続算学小筌」でも、同じように考えたのではないかと、爺は勝手な妄想を膨らましている＾＾；

それでは、「算法新書」とは、別の方法で、台形の高さ（小円の半径の4倍）を求めてみよう。

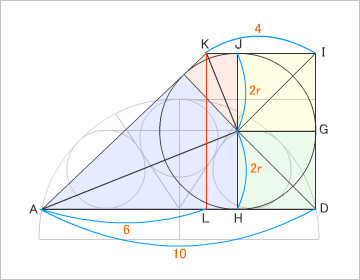
円が内接している台形の持つ「上底＋下底＝斜辺＋斜辺」となる性質を使う。台形の4つの頂点と内接円の中心を結ぶ。各辺の円の接点と内接円の中心を結ぶ。すると、三角形が8個できるが、各色どうしの三角形は合同（※今回の問題では、黄色と緑も合同）。つまり、上底と下底、それに2つの斜辺は、同じ長さの辺を持つ三角形の組み合わせで出来ているのね。

……というわけで、同じく「r=(10/7)」という答えを求めることができた。でも、やっぱり「続算学小筌」＆「算法新書」の「調和平均になる」という解法のほうが、日本的(?)で、美しい感じがする＾＾；

それにしても、なぜ、番組では、テーマが「和算」なのに、和算の解法のほうを紹介しなかったのだろうか？　もしかして、「和算」に興味を持ってもらうため、あえて「謎」としたのかな。番組では解説の時間が限られているから、ヒントを出すにとどめ、あとは自分で考えてね……ということかな。「謎」を提示されると、気になるよね。竹内センセの策略に、爺がみごとにハマってしまった……とゆーこと？？

※たけしのコマ大数学科の「過去問題」はこちらから。
■コマ大数学科：2009年度全講義リスト
■コマ大数学科：2008年度全講義リスト
■コマネチ大学数学科：2007年度全講義リスト
■コマネチ大学数学科：2006年度全講義リスト

■コマ大数学科DVD-BOXガイド

---