■コマ大数学科150講：ペンローズ・タイル

　ペンローズの「漁師脳」ではなく、「量子脳」理論は、爺にとって「思考の地平線」の向こう側＞＜； ちっとも理解できないが、黄金比が含まれる「ペンローズ・タイル」の美しさは、爺にもわかる？「たけしのコマ大数学科」

問題：１辺の長さが１の正ｍ角形の各辺の外側に１辺の長さが１の正ｎ角形を１つずつくっつけたとき、くっつけた正ｎ角形の隣り合う２つが１辺を共有するようなｍ、ｎの組として考えられるものをすべて求めなさい。

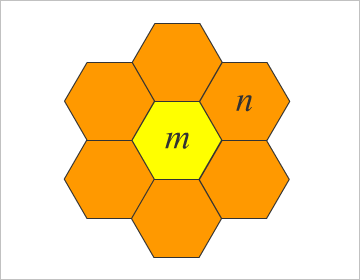
そのうちのひとつが、問題図にある、(m,n)=(6,6)の場合。これ以外の組み合わせを考えよ、ということね。

　コマ大数学研究会は、困ったときの「折り神さま」、「折り姫さま」とゆーわけで、文京区にある「おりがみ会館」へ。ところが「折り神さま」こと小林一夫館長と、「折り姫さま」こと、湯浅伸江先生は、大変忙しいとのことで、代わりにプロマジシャンの柏原由興さんが相手をしてくれた。

　柏原さんの教えを乞いつつ、また、過去のコマ大数学科のDVDで復習しつつ、いろいろな正多角形を作り、検証した。

　コマ大生はこんな形を作った。

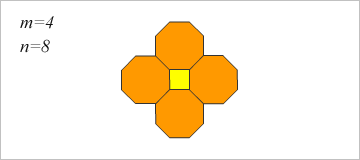
　正方形と正8角形の組み合わせで平面を並べ尽くすことができる。

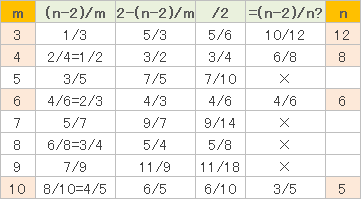
　マス北野は、ずっと電卓を離さず、計算していた。たとえば、正三角形の内角は60°、各辺に隙間ができぬように並ぶとすると、正ｎ角形の内角は、(360-60)/2=150°ということになる。これを正ｎ角形の内角の総和を求める式に当てはめると、
180(n-2)=150n
180n-150n=360
30n=360
n=12
となり、正12角形という答えを求めることができる。
同様の計算で、m=4、m=5のときを求める。マス北野の出した答えは、
(m,n)=(3,12)
=(4,8)
=(5,10)
正6角形の場合は、(6,6)となるが、これを超えると、計算の答えが整数ではなくなるので、これ以上はないと考えた。

　ところが、正5角形(m=5)で計算してみると、どうも計算が合わない。

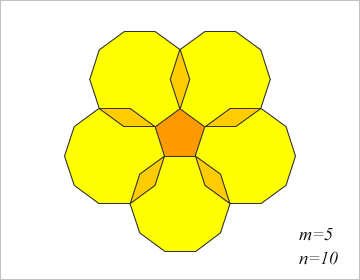
　実際に図を描いてみると、一目瞭然。正5角形のまわりに正10角形を並べると、重なってしまい、一辺を共有できない。いつもは、作図する、マス北野だが、今回は電卓のみの計算だったので、どこかで、「m」と「n」を取り違えてしまったのかも。

　木村美紀と山田茜さんの東大生チームも、考え方はマス北野と同じ。正ｍ角形の内角と、一辺を共有する、2つの正ｎ角形の内角を足すと、360°になる。この関係に着目して、方程式を立てた。

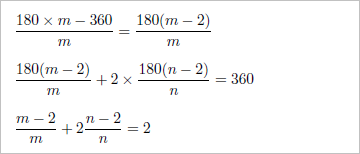
　この式の「m」に順に3、4、5…と代入して、「n」の値を調べ、(m,n)=(6,6)を含め、4つの答えを見つけた。
(m,n)=(3,12)
=(4,8)
=(10,5)

　で、これ以外の解はないという証明だが、n=4の正方形の場合は、2つの内角の和は180°になり、正ｍ角形の内角は180°になってしまうことから、n<5では、成立しないことを証明。

●中村亨センセの「美しき数学の時間」

解法(1)は、マス北野、東大生と同じ。以下、その手順。
(1)正ｍ角形を決める。
(2)正ｍ角形の内角を求める。
　（180°を単位にすると計算がラク）
　（m-2)/m*180
(3)360°(=2*180°)から(2)を引く。
(4)(3)を2で割る。
(5)(4)=(n-2)/nとなる「n」があればOK

解法(2)は、東大生の立てた方程式をもう少し整理したものだ。

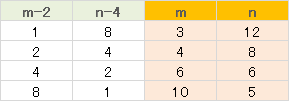
　ふたつの整数を掛け合わせて「8」になる組み合わせは、上の表の4通り。同時にこれ以外の別解がないことも証明される。

　ちなみに、正三角形と正12角形を組み合わせて並べると、以下のようになり、平面充填できる。

　正10角形と正5角形の組み合わせでは、平面を埋め尽くすことはできない。

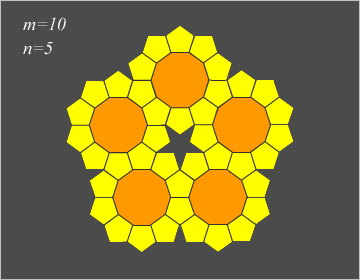
　コマ大フィールズ賞は、完璧な解答で東大生チームへ。

　今回のテーマの「ペンローズのタイル」だが、規則的な平面充填ではなく、非周期の平面充填というところがポイント、現実にペンローズ・タイルと似た「準結晶」構造が発見されるなど、興味深いのだが、爺の体力の限界；；　「ガスコン研究所」の過去記事を参照してほしい。

●第17回：エッシャー

●補習：ペンローズ

※Pencil Missaileは、[SPACE]キーでも発射できるよ＾＾；

※コマネチ大学数学科の「過去問題」はこちらから。
■コマ大数学科：2008年度全講義リスト
■コマネチ大学数学科：2007年度全講義リスト
■コマネチ大学数学科：2006年度全講義リスト

---