東京六大学に挑戦シリーズの第三弾。これまで、早稲田、明治に挑戦して、マス北野、東大生チームは敗退してきた。今回は、「飛べ飛べ戸部洋子」アナの母校である、立教大学に挑戦だ。
問題:縦、横の長さがそれぞれ、1、2の紙がある。幅Xで縦に切り、2つの紙片を作り、それぞれを丸めて2つの円柱の側面を作る。ただし、縦、横どちらの側を底にするかは、円柱の体積が小さくなるように決めるものとする。この時、2つの円柱の体積の和の最小値と、その時のXの値を求めよ(ただし、のりしろは考えなくてよい)。
※立教大学 法学部 (1996年入試問題)
長方形の紙を丸めて円柱を作るとき、長い辺を丸めるか、短い辺を丸めるか、2通りの方法がある。つまり、2枚の紙×2通りで、4通りの円柱が考えられるけれど、どちらの場合も、体積が小さいほうの円柱を採用するってことね。問題は、青と赤の円柱を足した体積が、最も小さくなる、Xの長さを求めよ……ということ。
立教大学は、戸部ちゃんの母校とゆーことで、「元ミス立教」の戸部アナも、コマ大数学研究会のロケに参戦。甘酸っぱい青春の思い出も披露しつつ、コマ大生が向かったのは「立教大学 放送研究会 アナウンス部」。なんでも、立教大学出身者には、「みのもんた」、「徳光和夫」、「古舘伊知郎」など、キャスターやアナウンサーを多く排出しているとのこと。
で、今回の問題に挑戦してもらうのは、社会学部2年生の大橋駿介さん。コマ大生、戸部ちゃん、アナウンス部の仲間が見守る中、大橋さんの出した答えは、「最小の体積の和は、「7/16π」、そのときのXの値は「1/2」と「3/2」。計測タイムは「9分35秒」だった。
ここから、マス北野と現役東大生の挑戦が始まる。
今回の東大生チームは、小橋りささんと、岡本麻希さん。まず、円柱の底を縦にするか、横にするかで、できる4つのパターンの円柱の体積を式に表す。
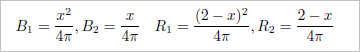
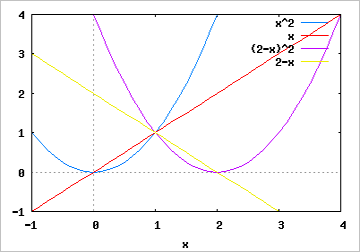
分母の「4π」は共通なので、分子の部分を抜き取り、y=x^2,y=x,y=(2-x)^2,y=2-xのグラフを描く。
0~1以下と、1~2未満に分けて最小値を求める。
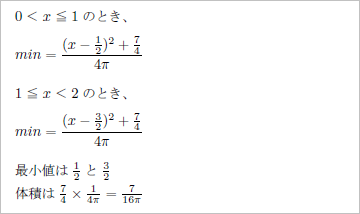
「平方完成」すると、カッコで括られた二乗部分は、正の数であり、二乗部分が「0」のときが、一番小さくなる。というわけで、最小値は(1/2)と(3/2)、そのときの体積は(7/16π)になった。東大生チームのタイムは「10分48秒」。
マス北野も今回は、正攻法で黙々と計算する。マス北野の解答用紙には、計算式が書き込まれていくが、頭の中で計算した結果をメモする感じで、空白を見つけると、そこに計算式を書くため、計算式は重なり、順序もよくわからない。そこで、マス北野の説明を頼りに、マス北野の思考の流れを爺が「Maxima」で追ってみた。

マス北野も円柱の底をどこに取るかで4つのパターンに分けた。解答用紙にあった数式は、東大生の分類で言うと、B1+R2になる。竹内センセの説明では「体積(2)の式」(後述)、東大生は、最小値を求めるのに「平方完成」を使ったが、マス北野は「微分法」を使った。マス北野の答えも、最小値は(1/2)と(3/2)、そのときの体積は(7/16π)。所要タイムは「8分55秒」だった。
・立教(大橋さん):正解(9分35秒)
・東大生チーム:正解(10分48秒)
・マス北野:正解(8分55秒)
マス北野が「コマ大フィールズ賞」を獲得した。
●竹内薫センセの「美しき数学の時間」
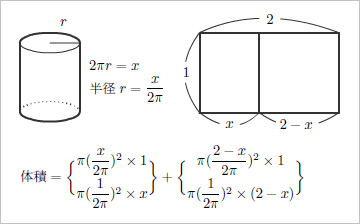
「x」を円柱の底とすると、円周は「2πr=x」、半径(r)は「x/2π」となる。円の面積は「πr^2」なので、それに高さ「1」を掛けたものが円柱の体積になる。「1」を円柱の底にすると、半径(r)は「1/2π」、高さが「x」となる。同様に、長方形の長辺「2」から「x」を切り取ったほうの紙の体積を求める式を作る。

(2通り)+(2通り)の計算式を「平方完成」の形にして、最小値を求める。
竹内薫センセは、最小値を求める方法として「平方完成」を使うか、「微分」を使うかで、1~2分の差が出るかもしれないと言っていた。
番組で、東大生の鉛筆を動かす速さを見ると、計算スピードにおいて、マス北野は、東大生チームに勝てないだろう。しかし、問題をどのように解いたらいいかという引き出し(知識)と、ひらめき(直感力)があると思う。前講義(145講:可視領域)でも、三角形の三頂点と、もうひとつ30度で見える点が円周上にあることを見抜いていた。
今回の問題で言えば、マス北野は、いきなり解答用紙に体積(2)の計算式を書いていた。体積(1)と体積(4)は同じ辺を丸める方法で、とくに体積(4)は「1」の辺を丸めて円柱を作るので、どこで切っても足し合わせた体積は変わらない。
で、最小になる組み合わせは、どう考えても、短い方の辺を円柱の底にしたほうが体積は小さくなるはず。つまり、「X」が1以下なら、「X」の辺を丸めて円柱の底にする。逆に「X」を切り取った残りの紙は、「2-X」で1より大きいので、「1」の辺を丸めて円柱の底にする。そう考えると、体積(2)、体積(3)の方法になるのは直感的にわかる。
そして、体積(2)で、「X」が「1/2」と求まれば、「2-(1/2)」で、もうひとつの値は「3/2」と必然的に求まる。
「それは結果論」、あるいは、「マス北野に対する判官贔屓じゃないの」と言われてしまうかもしれないけれど、数学的なセンスというのは、そーゆーもんじゃないかな。
※Pencil Missaileは、[SPACE]キーでも発射できるよ^^;
※コマネチ大学数学科の「過去問題」はこちらから。
■コマ大数学科:2008年度全講義リスト
■コマネチ大学数学科:2007年度全講義リスト
■コマネチ大学数学科:2006年度全講義リスト

再び書き込ませていただきます。
1より小さな数はかければかけるほど小さくなり、1より大きな数はかければかけるほど大きくなるので、
x<1 とすれば 2-x>1となり、
東大生チームの式で言えば
B1<B2、R1>R2 となります。
また、x<1の時のB1、B2はそれぞれ
x>1のときのR1、R2と同じになります。
以上長々と書きましたが、これは閃きや直感と言うより、むしろ論理的な数式の評価であると言えるのではないでしょうか。そしてこれこそが、数学ではもっとも大切なことである、あるいは数学の醍醐味であると思います。
毎回楽しみに見させていただいています。今回もマス、東大チームの分析に関し丁寧な分析かつ解説に頭の下がる思いです。
東大チームの解法は分類分けとして0
今回は、解きがいのある問題でした。
x<1 と x>1の場合でそれぞれ
長い方を底にした場合から短い方を底にした場合を引くと答えがどちらとも正になるので短い方を底にする方が体積が小さくなるのが分かりました。
私の場合は、平方完成をした為同時に体積も求まってしまい、マス並みの速さで解答できたと思います。
ただし、3/2の方の解が抜けてしまいました。
答えは1つではないという意識をしないといけなかったと反省しました。
再度、おじゃまします。
この回も見たのですが、やはり4つの場合分けは無駄な
作業に思われます。
辺をaとbとした場合、体積はa^2*b*定数または
a*b^2*定数となるので、丸めるのは常に短い辺固定。
かつx<=1としても一般性は失われないので、と前提を
つけると丸め方も決まってしまいますから、
x^2*1+1^2*(2-x)の極値を求めればよく、微分して
x=1/2が出てしまうので、あとは普通に円柱の体積を求めて、
とやると、2分もかかりませんでした。
ただ、「す」さんと同様、一般性を失わないはずの
仮定をつけたために、3/2は答えとしなかったところが
いけないところでした。
可視域でも思ったのですが、東大生チームは無駄に計算量を
増やしているように思います。特に、ここのところ小学生の子供の
算数を見ている関係上、強くそう思うのかもしれません。