前回の「コマ大数学科141講:原始ピタゴラス数」の記事をアップしたあと、マス北野の解法を検証してみた。どうやら、爺は、マス北野の解法を理解できず、勝手な解釈を加えていたようだ><;
番組内で、マス北野は「奇数を足していくと、累乗の形になる」と言っていた。たとえば、a=3としたとき、1~3^2(9)までの奇数をすべて足す。1+3+5+7+9=25で、25の平方根をとると、c=5、bは、cから1を引く。b=4 というわけで、(a,b,c) = (3,4,5)となる。
マス北野の方法で、辺「c」を求め、「b=c-1」として、「b」が定まった時点で、ピタゴラスの定理「a^2+b^2=c^2」を満たしているか、辺「a」が3以上100以下の素数の場合を調べたが、すべて条件を満たしていた。
マス北野の「奇数だけを足していくと平方数になる」というのは、「四角数」と呼ばれるもの。
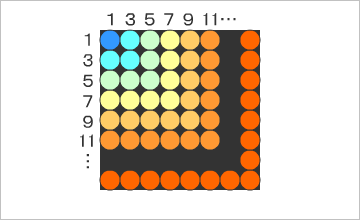
碁石を正方形に並べるとき、一辺の大きさを碁石1個分ずつ増やしていくと、新たに必要な碁石は、必ず奇数になる。出来上がった正方形の碁石の数(合計)は、平方数になるわけだ。
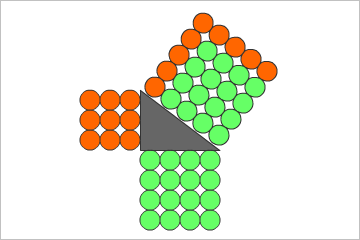
ピタゴラスの定理は「a^2+b^2=c^2」なので、原始ピタゴラス数も、四角数(平方数)を組み合わせることで、作ることができる(ただし、辺の長さが互いに素という条件を満たさなければならない)。また、直角を挟む二辺「a」と「b」は、交換可能だが、原始ピタゴラス数の定義から、必ず、偶奇に分かれる。
今回の問題は、原始ピタゴラス数のうち、二辺が素数の場合、マス北野の方法を、辺「a」に3以上の素数に適用していくと、辺「c」が素数になるかどうかは、分かれるが、少なくとも「a」は、素数なので、「a」と「b」、「a」と「c」は、互いに素。そして、「b」と「c」の差は「1」なので、互いに素。検証した(a,b,c)は、すべて原始ピタゴラス数であることは、間違いない(ただし、「a」は、3以上の素数、2のときは、除く)。
ただ、肝腎の「なぜそうなるか?」を爺は、数式を使って証明することができない><;
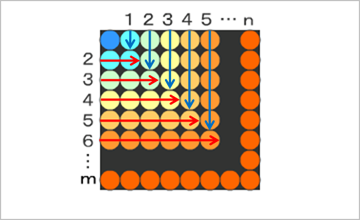
碁石の数を「m」は横に、「n」は縦に図のように数え、これを原始ピタゴラス数を求める式に当てはめてみる。
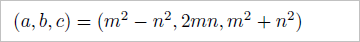
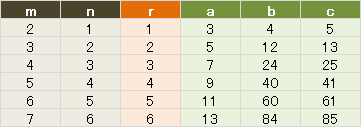
※「r」は、直角三角形に内接する円の半径ね(前回の記事を参照)。しかし、これは、爺の妄想も甚だしい。奇数を差が「1」のふたつの数に分けるわけだから、「m」と「n」が互いに素になるのは、当たり前ちゃ、当たり前だ><;
ピタゴラスの定理から、原始ピタゴラス数を作る式の一般形を求める過程は、結城浩さんの「数学ガール フェルマーの最終定理」に詳しい。結城浩さんは、これを『ピタゴラ・ジュース・メーカー』と命名。「m」と「n」というフルーツを入れると、おいしい「原始ピタゴラス数」というジュースが自動的に出来上がるわけ。
