フジテレビのアナウンサーにも派閥が存在するという。ちなみに、戸部アナは、軽部派の一派だそうな^^;「たけしのコマ大数学科」
問題:5人の政治家がいて、いくつかの派閥があります。派閥とは1人以上の政治家が属する集団のことです。2つの派閥は、もし、その両方に属する政治家と、どちらにも属さない政治家が共に存在すれば、必ず、一方が他方を含むとします。派閥の個数の最大値を求めなさい。(ただし、5人全員からなる集団も派閥であるとします。)
※出典:2004年日本数学オリンピック予選問題
問題文では、「いくつかの派閥があります」とあるが、5人の政治家がいるなら、1人1派閥で、最大でも5個だろう…と爺は思ってしまった。でも「必ず、一方が他方を含む」とあるので、5人全員の派閥1つか、最大でも2つの派閥になる。問題の意図は、5人の政治家で可能な組み合わせをしたときの派閥数の最大値ということね。
コマ大数学科は、ダチョウ倶楽部の上島竜平を講師に迎え、芸能界の派閥についての講義を受けるが、まったく役に立たない^^; そこで{上島, 出川, 勝俣, 今田, 関根}という5人でできる可能な派閥の数を数えた。たとえば、ヘンタイ派={上島}という派閥と、ノーマル派={出川, 勝俣, 今田, 関根}というよーな派閥だ。さまざまな組み合わせを検証した結果「35」という答えになった。
マス北野は、2つの派閥を構成する人数に注目した。

(5+4+3+2+1+0)×2として、派閥の組み合わせ数を30通りと考えたが、「その両方に属する政治家と、どちらにも属さない政治家が共に存在すれば、必ず、一方が他方を含むものとします」という条件が気になり、30通りの半分で「15」通りという答えを出した。でも、「あやしいなぁ…」とつぶやく。
木村美紀、山田茜さんの東大生チームは、「ベン図」を描いて問題を解決しようとした。「ベン図」というのは、イギリスの数学者、ジョン・ベンによって考案された、集合の包含関係を図式化したもの。
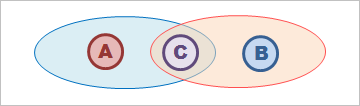
東大生は、上の図のように両方の派閥に属する政治家(重なる部分)があると、条件を満たさないと考えた。つまり、派閥どうしが重ならない集合だ。
数え方はよくわからないが、「9個」という答え。
●中村亨センセの「美しき数学の時間」
まず、問題の「2つの派閥A,Bに、共に属する人と、共に属さない人がいるとき、一方が他方に含まれる。」という条件を、もう少し噛み砕いて、言い替えてみる。
以下の条件が1つでもあてはまれば、オーケーだ。
(1):AとBに共に属する人はいない(重なっていない)。
(2):AとBに共に属する人がいるとき、AとBに共に属さない人はいない(つまり、派閥から外れた人はいない)。
(3):AとBに共に属する人がいて、AとBで全員にならないとき(AがBに含まれるか、AがBを含む)。
AかBの2つの派閥に属するかは、2通りの選択肢が5人の政治家にあるので、2^5-1=31通りの派閥がある。マイナス1としているのは、誰も派閥に属さないという、空集合を取り除くため。マス北野の場合は、逆に5人全員が1つの派閥{0,1,2,3,4}を考慮しなかったのかな……(?)。ここから条件によって絞り込むわけだが、中村センセの説明によると、
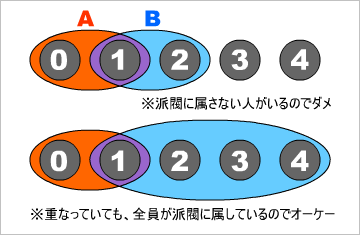
※0~4の数字は、A,B,C…と同じく、政治家の背番号だと思ってほしい。
上の図のように2つの派閥に共に属する(重なっても)オーケーということだが、爺が考えるに、問題は組み合わせパターンの数ではなく、派閥の数を数えることである。
たとえば、A={0,1} と B={1,2,3,4}の2つの派閥は、派閥どうしが重ならないことを条件にカウントしたとき、
A={0} B={1,2,3,4} ※B派閥はすでに存在する。
A={0,1} B={2,3,4} ※A派閥はすでに存在する。
…ということにならないだろうか。
つまり、重複カウントになってしまい、結局は、東大生のように、派閥どうしが重ならないパターンを数えればいいのでは……?(疑問符だらけだ><;)
A派閥が1人で、残りはB派閥
{0 } { 1,2,3,4}
{ 1 } {0, 2,3,4}
{ 2 } {0,1, 3,4}
{ 3 } {0,1,2, 4}
{ 4} {0,1,2,3 }
これで、10個。
A派閥が2人で、残りはB派閥
{0,1 } { 2,3,4}
{ 2,3 } {0,1, 4}
足して14個。
最後に5人全員の派閥。
{0,1,2,3,4}
合計「15」。
というわけで、マス北野は「わけがわかってないのに正解するとは、すごいな」と言っていたが、コマ大フィールズ賞は、不正解であったけれど、考え方を評価して、東大生チームが獲得した。
番組終了後も、とゆーか、この記事を書いている時点でも、なぜ、{0,3}とか、{1,2}のような派閥は存在できないのか。爺は悩んでしまった;; すでに{0,1}という派閥が存在した場合、共に属する{0,3}や、{1,2}という派閥があると、どちらにも属さない政治家がいるということになり、条件を満たさなくなってしまうということに、やっと気がついた><;
で、出典元の「数学オリンピック2000~2005」の問題をあらためて読み直してみると、政治家の人数は7人だった。
※以下、引用
正の整数 h に対し、h 人の政治家の集合 S 上の強い入れ子をなす派閥の個数が 2h-1 以下であることを、h に関する帰納法で示す。
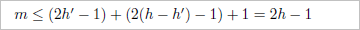
問題文の状況を一般化し、2以上の整数 k について、K 人の政治家の集合 S 上で弱い入れ子をなす派閥の個数が 4k-5 を超えないことを示す。
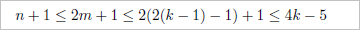
※引用終わり
「強い入れ子」とか「弱い入れ子」とか、文字だけだと、どんなイメージなのか、爺にはよくわからない;;
東大生は、条件を絞りすぎ、「強い入れ子」の状態を考えたのかな…?? 政治家5人の場合、「2h-1」に代入すれば、「9」となり、答えが一致する。
一方、中村亨センセの解説にあったように、派閥Aと派閥Bに共に属する人がいても(重なる部分があっても)、派閥に属さない人がいなければ、オーケーというのを、「弱い入れ子」の状態と考えれば、「4k-5」に「5」を代入すれば、答えは「15」となる。
さて、ちょっといい話(数学のトリビア)は、「集合論」の話。コマ大数学科135講「長文読解」で、竹内薫センセが「カントールの対角線論法」を紹介してくれたが、爺には、題目とのつながりがよくわからなかったけれど、じつは「集合論」つながりだったのね。
で、初期の集合論は、いろんな批判に晒された時期もあったという。そのひとつが、有名な「ラッセルのパラドックス」というもの。中村亨センセが紹介してくれた例とは、ちょっと違うけれど、こっちのほうがおもしろいと爺は感じた。
ある村に床屋があった。床屋は「自分で髪を切ったり、髭を剃ったりしない人の、髪を切り、髭を剃る」のが仕事だ。村は、自分で髪を切り、髭を剃る人(床屋に行かない人)の集合と、自分では髪を切らず、髭も剃らない人(床屋へ行く人)の集合に二分される。それでは「床屋」は、どっちの集合に属するのか?
う~む、自分で髭を剃ったら、床屋は、自分で髭を剃る人の髭を剃ったことになるし、床屋として自分の髭を剃ったとしても、自分で髭を剃らない人の集団に入るとも思えない。
これを数式で表すと、

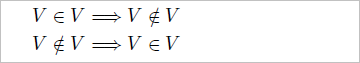
つまり、VがVの要素であるならば、VはVに属さないし、VがVの要素でないならば、VはVに属するという矛盾が生まれる。
結論を言うと、ラッセルのパラドックスは、集合の命題の体をなしていないということ。カントールが「集合論」を唱えたのは1870年頃らしいが、20世紀に入り、現代的な「集合論」が確立した。めでたし、めでたし^^;
爺のちょっと、とほほな話。番組のテロップで(0,1)(2,3,4)のような表記がされていたけれど、(1,2,3)と書くと、順番も考慮するが、{1,2,3}と書くと、順番は考慮しない、という数学のお約束を最近知った。(40年遅いわ><;)
 数学オリンピック2000‐2005 (財)数学オリンピック財団/編 発行:日本評論社 価格:2100円+税 発行年月:2005年10月 ISBN:4-535-78453-1 |
※Pencil Missaileは、[SPACE]キーでも発射できるよ^^;
※コマネチ大学数学科の「過去問題」はこちらから。
■コマ大数学科:2008年度全講義リスト
■コマネチ大学数学科:2007年度全講義リスト
■コマネチ大学数学科:2006年度全講義リスト
