「♪おくせんまん、おくせんまん、ジャパーーン♪」と、なげやりな戸部アナの前フリで始まった「たけしのコマ大数学科」。今回のお題は「億」。
問題:1から1億までの整数の中に出てくる、すべての数字の和を求めよ!(※追記:たとえば「109」なら、1+0+9=10のように数字に分解して足していく)
まったく役に立たないが、整数の中に出てくる数字を足していくFlashを作ってみた。白の枠内の数字をダブルクリックして、キーボードから数値を入力後、[START]ボタンを押してね。中村亨センセによると、1~1億までに出現する数字を、もしも、1秒間にひとつずつ足していくと、25年ぐらいかかるそうな><;
まずは、コマ大数学研究会の挑戦。壁や天井、テーブル、柱など、一面に数字が書き込まれた部屋に閉じ込められ、ひたすら電卓を叩いて計算する。助っ人として呼んだ「電卓名人」も途中で帰ってしまう。結局、5時間以上かけて、1万まで数え上げる。コマ大生によると10000までの数字の総和は「180001」。1億は1万×1万なので、答えは「18億1万」となった。じつは、〆さばアタルが、すばらしい発見をしたのだが、それは、後ほど紹介する。
お疲れのマス北野は、計算式を立てると、計算はポヌさんにまかせてしまった。しかし「時間内に計算できるかなぁ…」と弱気。考え方としては、
0~9までを足すと45
10~19までを足すと、45+10
20~29までを足すと、45+20
…ということなのだが、途中で息切れ。
ポヌさんが掲げたフリップには、
「45*10^7+(10/2)*(10^7-1)*10^7+1」
と書いてあったように思うが、よくわからない計算式だ。
木村美紀と岡本麻希の東大野望めらめらシスターズは、0~9までを足した数(45)を「x」とすると、
0~99は、20x
0~999は、300x
0~9999は、4000x
というふうに増えていく。このぶんでいくと、
0~99999999は、80000000xとなる。
つまり、80000000×45=3600000000(36億)
そして、1億の「1」を足して、答えは、
「3600000001(36億1)」
爺は、この問題を見たとき、どっかでやったことがあるぞと思った。それは、過去記事の
このときは、整数の「1」の数を数えた。もしも、「1」の数をすべて数える関数があったとすると、f(99)=20になる(1の位に10個+10の位に10個で20個)。さらに「999」では(100+100+100)で、f(999)=300だ。このことから、桁数を「k」とすると、f(9999…)=k*10^(k-1)と予想した。つまり、1億-1は、8桁なので、
f(99999999)=8*10^7=80000000
これは「1」だけを数えた数なので、0~9までを足した数「45」を掛けて、80000000×45+1=3600000001(36億1)という答えに辿り着いた。
さて、中村亨センセの「美しき数学の時間」だ。
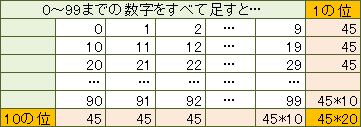
これは、マス北野や、東大メラメラ・シスターズの考え方と同じ。0~99に含まれる数字の和は、1の位、10の位に分けて数えると、45が10個ずつで、45×(10+10)になる。同様に0~999の場合は、45×(100+100+100)だ。地道に8桁まで数えれば、45×(10000000×8)。これに1億の「1」を足した数が答えになる。
アタルのひらめきに、中村センセはドキッとしたという。アタルは、それぞれの桁の数字を足した一番大きな数は、9+9+9+9+9+9+9+9=72 で、平均すると36になることに気付いた。しかし、そのあとがいけない。36×5000万として、18億としてしまったのだ。たぶん、コマ大生の答え「18億1万」にひきづられてしまったのだろう。平均した時点で「2」で割っているので、そのまま、36×1億+1とすれば、正解だったのだ。
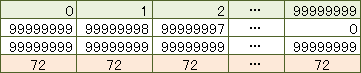
等差数列の和は「((初項+終項)÷2)×項数」で求めることができるが、0~99999999の数字の和は、
(((0+9)×8桁)÷2)×項数(1億)で求めることができるわけね。
せっかくのすばらしいひらめき、アタル・チャーーンス!だったのに正解には至らず、コマネチ・フィールズ賞は、正解した東大野望めらめらシスターズが獲得した。
《11月5日追記:蛇足》
冒頭の中村センセの「1秒間にひとつずつ足していくと、約25年かかる」という話だけれど、最初の「0」と最後の1億の「1」を帳消しにして、数字の数は、8000万×10個で8億個。つまり、1秒間に1個なので、かかる時間は、8億秒。これを分、時、日で割っていくと、
80000000÷60÷60÷24÷365.2422≒25.351年となる。
ところで、コマ大数学研究会は、1~10000までに出現する数字を足した。ロケ時間を5時間とすると、およそ、4.5秒に1回、計算したことになる。このまま、1億までの数字を足していくと(寝食も忘れて、ひたすら計算しても)約114年かかることになる。
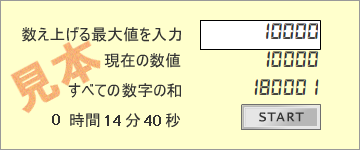
爺はコマ大生の「実際に確かめてみる」という姿勢にシンパシーを感じているが、コマ大生ほどの体力がないので、冒頭のFlashを作成した。コマ大生と同じく、ひとつひとつ出現した数字を足しているが、爺が検証した結果では、14分40秒かかった(システム環境によって多少の違いが出るかもしれない)。それにしても、40000個の数字の足し算をコマ大生は、間違わずに計算したことに驚かされる。爺だったら、途中で絶対、電卓のキーを打ち間違えると思う。
で、爺の作成したFlashでは、およそ、0.22秒に1回の割合で計算したことになる。つまり、1秒間に5回弱だ。Flashの設定値に「100000000」(1億)と入力した人がいるかもしれないが、その人は結果をまだ得られていないはず。だって、1~1億に出現する、すべての数を足すには、5年半以上もかかるんだもの><;
《追記:11月16日》
■cccktさんの方法(※コメント参照)で検証してみた。
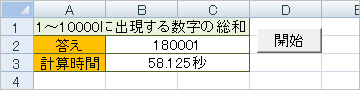
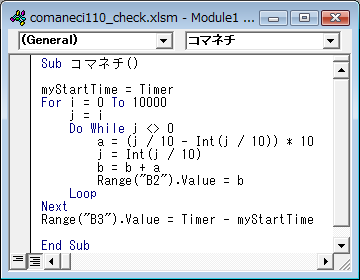
For~Nextでループさせると、CPUは計算に没頭してしまい、その間、無反応になってしまう。爺はそれが怖いので、コマ大生と同じく、1~1万に出現する数字の和で検証。爺の場合は、計算結果を逐次表示しているので、およそ58秒(非表示にすると、0.029秒だった)。エクセルの場合は、CPUの性能に大きく影響される(数値の型はデフォルトのバリアント型のまま、型宣言をしても、あまり計算速度には影響がないみたい)。
Flashが遅いのは、ブラウザーで表示することを前提としているため。ポリシーは、CPUパワーを独占しないこと。「for~」で1億回もループさせたら、確実に警告を発し、怒られる。そのため、フレームを表示するごと(デフォルトで、1/12秒ごと)に、計算ルーチンを呼び出すようにしている。
 たけしのコマ大数学科DVD1 (第1期) |
 たけしのコマ大数学科DVD2 (第2期) |
※コマネチ大学数学科の「過去問題」はこちらから。
■コマネチ大学数学科:2006年度全講義リスト
■コマネチ大学数学科:2007年度全講義リスト

問題を「1~1億の整数の和は?」だと間違えてて正解に納得できませんでした(笑)
胸のつかえがとれました…ありがたい
3,600,000,001は本当に正解なのでしょうか?
もっと大きな数字ではないでしょうか?
答えはもっと大きな数字じゃないですか?
問題の意味がわからなくて…
1+2+3+4+5+6+7+8+9+10+11+12+13+14+etc…100000000ってことですか?
名無しさん、まささん、ぺいこさん、コメントありがとうございます。
またまた、ココログの「コメント投稿通知」メールが届かず、コメントの公開が遅れてしまいました。ごめんなさい;;
この問題を「整数の和」と誤解した人は多いようですね。11なら、1+1=2、12なら、1+2=3のように、ひとつひとつの数字に分解して足していくということです。
そういうふうに考えると、1億-1は、99999999ですから、9が8個で72になります。0~99999999の1億個の数値は、ひとつひとつの数字を足し合わせると、最小値が「0」、最大値が「72」であることは明白で、どの数値も必ず「0~72」の範囲になるわけです。「109」と「901」は、どちらも分解した数字を足し合わせると「10」です。
つまり、平均を取ると「(0+72)÷2=36」、これが1億個あり、最後の1億の「1」を足すと「36億1」というわけですね。
はじめまして。
私はこの問題は簡単に解けたのですが、
先生の説明や東大生の回答とは違う法則(?)で問いた気がしたのですが、
学がないので本当に違う法則かどうか教えて頂けるとありがたいです。
この問題を聞いたとき
000…0001
000…0002
:
999…9999
という表を描き
10までなら
100までなら
という考え方がわずらわしかったので
一の位と1千万の位を縦(桁別)に見ました。
一の位は
1
2
3
:
0を1千万回繰返す。
1千万の位は
00:
01
1
:
1
と1千万づつが各数字1回出現する。
要するにどの桁も各数字が出現する回数は同じということに気付きました。
あとは単純計算ですね。
基本的に学はないのでよくわかりませんが、このとき方は東大生と同じなのでしょうか?
マミタソさんコメントありがとうございます。
(※マミタンではないんですね^^;)
桁ごとに各数字の出現数に注目する点で、マス北野や東大生の解法と基本的には同じだと、爺は思います。
いきなり、8桁の数字の表を描くのは大変なので、少ない桁数で数値と個別の数字の関係を検証していき、一般的な法則を導きます。これを数学的帰納法って呼ぶらしいですよ。
桁ごとに各数字の出現数に注目すると、
2桁→10+10=20
3桁→100+100+100=300
4桁→1000+1000+1000+1000=4000
となることから、桁数×10^(桁数-1)を導き、
8桁の場合は、1000万が8個で、8000万となるわけです。
この思考過程を面倒と思うかどうかは、個人次第なのですが、問題解決の手法として、できるだけ単純化して考え、それを展開していく方法がよく用いられます。
でも、人によっては、頭の中だけで無意識にこれらの論証を行い、マミタソさんのように、途中の思考過程をとばして、直感的に解法がひらめく人もいると思います。
その「ひらめき」を爺にもおすそ分けしてほしいほどです^^;
はじめまして。
地域の都合上、先ほど放送を見ました。
放送の最後の方まで、只の等差数列の和と勘違いして、一体何故こんな問題が???と思って見てました。
で、やっと題意に気づいて、急いでテレビを消して(解答をはじめていたので)解きました。
やり方はマミタソさんと同じです。マスを8個並べて、各マスに0-9までの数字が動き回るところをイメージすれば、このアイデアが出てきます。
また、この解法の良いところは、東大生のような帰納的なやり方と異なり、証明が要りません。(数学的に厳密なことは自明でしょう)
と、偉そうな事書きましたが、私自身は桁数の8で掛けるのを忘れて、何で答えが合わないかさんざ悩みました。 年を取って、発想力はどんどん伸びてますが、ミスが洒落にならないレベルに。。。
そんな私だからこそ断言します。あの10000までの手計算はヤラセです。80000回のキータッチをミス無く?そんなのは確率的にありえない!!!もしやるなら、100個くらいのクラスターに分けて、各クラスターを5人位にやらせて4:1だったら4を正解に、一致人数が4人以下だったらやり直し。その結果を合計する。それぐらいやらなけりゃ無理ですよ。
エクセルマクロで、問題の計算を行うプログラム作成して見ました。
Long変数でも足りないので、合計が2億を超えないよう工夫してます。
計算時間5分ほどで正解がでます。
人間;数十年
コンピュータ;5分
演算能力におけるコンピュータの凄さにはいまさらながら驚きます。
ちなみに、プログラムも5分なので、
数学的に求めるより早かったです(^^;)
For i = 1 To 100000000
j = i
Do While j <> 0
a = (j / 10 – Int(j / 10)) * 10
j = Int(j / 10)
b = b + a
If b > 200000000 Then
b = b – 200000000
c = c + 1
End If
Loop
Next
cccktさん、コメントありがとうございます。
1億回のループですか……^^;
数値をひとつひとつの「数字」に分解するとき、爺は一度、文字列に変換してから1文字ずつ取り出していましたが、なんて、回りくどい方法を取ったものだと思いました。数値を数値のまま、取り出す方法を考えれば、よかったんですね^^;
爺もcccktさんの方法を検証してみましたが、コメント欄には、画像を載せることができないので、記事中に追記しておきます。
山梨では、昨日の夜中に放送されていて、珍しく夜更かしをしていたので、初めて見ました。面白い番組ですね。
整数の和は
X×X/2+X/2
(1億×5千万+5千万)
で出るので
昨日の問題は
(X-1の各数字の和)÷2×X+(Xの各数字の和)
72÷2×1億+1
で出しました。
素人なので、上手に計算式を表記できませんが…。
難しく考えるのが苦手なので、大きい数字と小さい数字を組み合わせたり、間を取ったり、という感じでできました。
皆さんより1年も遅れた古臭い話でしたが、偶然、昨日の気になったテレビの話題を見つけたので、つい投稿してしまいました。
山梨県人さん、コメントありがとうございます。
爺も「難しく考えるのが苦手」です^^;
難しいと感じる問題でも、できるだけ、やさしく考えたいですね。