■コマネチ大学数学科107講：スパイラル正方形

　サブプライムローンの破綻を端にして、アメリカ発の金融不安の連鎖は、世界的なスパイラル不況に落ち込んでいくのか「たけしのコマ大数学科」お題は「スパイラル正方形」

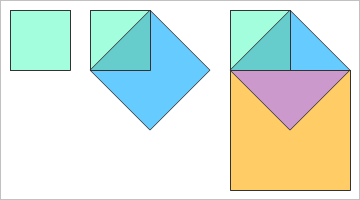
問題：一辺が10cmの正方形から始めて、その対角線を辺とする正方形を右回りに次々と描いていく。正方形を11個描いたときにできる図形の面積を求めよ。

　3本撮りロケの1本目ということで、コマ大数学研究会は、控え室でさっそく、10cm四方の紙から始め、対角線の長さの正方形を次々とつなげていくが、あっという間に、控え室には収まらなくない大きさになり、結局はスタジオに持ち込んで計測……＾＾；

　コマ大数学研究会のメジャーによる計測では、14.5285平方メートル。

　マス北野と崖の上のポヌさんコンビは、最初の正方形の一辺を「a」とすると、11個目の正方形は、「a(√2）^10」になり、1～10個の正方形は、半分が次の正方形に隠されることから、計算式を立てる。じつは、マス北野は、ロケのあった、この日、「クイズ・ミリオネア」の収録を終えたあとで、かなり疲れた様子。計算式を立てたあとは、ポヌさんに計算をまかせる。計算の結果は、153550平方センチメートル。

　東大理科三類の「秒殺シスターズ」、衛藤樹さんと、伊藤理恵さんは、今回もあっという間、秒殺で解答を書き込んだ。最初の正方形(10×10cm)から次の正方形の一辺は(√2)倍、面積は(√2)^2で2倍になることは明白。だが、じっさいに図形を描いてみれば、すぐにわかるのだが、8個目の正方形は、最初の正方形と重なってしまう。以降、9～11個の正方形は、2～4個目の正方形と重なってしまうので、面積は、5～11個の正方形の面積を考えればよいことがわかる。

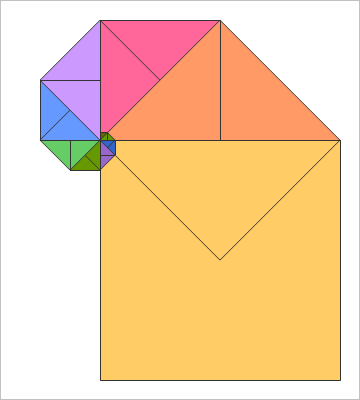
　東大生の計算式は以下の通り。
最小の正方形の面積は10×10＝100、その半分は隠れるので、50平方cm、この5番目から11番目の正方形の面積を計算すればよいのだから……。
50×(2^4+2^5+2^6+2^7+2^8+2^9+2^10)+50×2^10
カッコ内は等差数列なので、
50×(2^4×((2^7-1)÷(2-1))＋50×2^10
と表すことができる。
50で括ると、
50×(16×127＋1024)となり、
答えは、152800平方cmとなる。

　マス北野は、頭の中で、計算式を立てたので、実際に図形を描いたとき、8個目以降の正方形がすでに描いた正方形に次々と重なっていくというイメージを描ききれなかったようだ。

　もちろん、正解は「152800平方cm」で、まんまと、中村亨センセの思惑通り、その策術にはまった、マス北野とポヌさんは、コマネチ・フィールズ賞を逃し、東大理科三類の「秒殺シスターズ」、衛藤樹さんと伊藤理恵さんが獲得した。

　で、中村亨センセによる「美しき数学の時間」。基本的には、東大生チームの解答の通りなのだが、これを幾何的な図形問題として捉えると……。

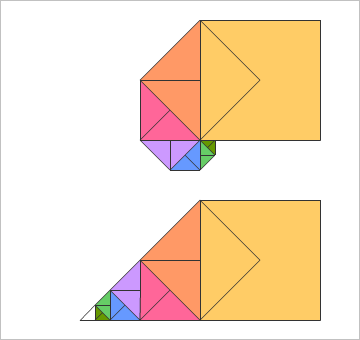
　上図のように、並び換えると、11個目の正方形の1.5倍の面積から、5番目の正方形の面積の半分を引いた面積が答えであることがわかる。

　つまり、求める面積は、
＝3/2(1.5倍)×(11番目の正方形の面積)－1/2(5番目の正方形の面積）というわけで、n番目の正方形の面積は、(2^n-1)なので……
＝(3/2)×(2^10)×(10^2：最初の正方形)－(2^4)×(10^2)
＝152800
と、答えを求めることができる。

　「ちょっといい話」では、対数螺旋の例として「ひまわりの種」や「オウム貝」を紹介していた。「かたつむり」はたった1対の遺伝子の違いで、殻の渦巻きが右回りと左回りに分かれるというのが興味深かった。

　「スパイラル正方形」の問題は、下記のサイトに、いろいろな人が解答を寄せているので、参考にしてほしい。

■数学の部屋
http://web2.incl.ne.jp/yaoki/week25.htm

---