北京オリンピックも終わたけれど、「まさか、北島康介が溺れるとはなぁ」とは、マス北野の弁(「たけしのコマ大数学科」は、北京オリンピック前に収録されたもの^^;)。
問題:直線に沿って1メートルおきに旗が13本立ててある。左端からスタートして、全部の旗をどこか1箇所に集めたい。ただし、一度に持てる旗は1本のみ。移動距離を最短にするには、旗をどこに集めたらいいか。また、その最短移動距離を答えよ!
【遊び方】旗の上についている数字は旗の数。どこか1箇所に集めると何本あるかわからなくなっちゃうからだ。[START]ボタンを押し、キーボードの[←]、[→]キーで移動。[↑]キーで旗を取り、同じく[↑]キーで旗を置く。13本の旗を1箇所に集めれば終了。赤い数字が移動距離。やり直すときは、[START]ボタンを押してね。
「花の東大生数学祭り」で最下位になり、罰ゲーム(?)で赤いジャージを着た山田茜のコマ大ロケ。夏のお台場海岸は、紫外線も多く。日傘をささないと、顔も日焼けして、まっかな「トマト」になっちゃうよ。(正確には「トマト」は、山田茜が所属するテニスサークルの名称)。砂浜に旗を立てて検証開始。トマトちゃん、じゃない、山田茜(コマ大数学研究会)の答えは、左から7番目に集め、移動距離は78メートル。旗が13本なので、真ん中が7番目の旗で、これを中心にして、左右6本づつの対称となる。もし、6番目に集めると、その対称位置にある8番目と答えが同じになり。答えが2つになってしまう。答えが1つに定まるのは、7番目。と説明したが、この説明は、明らかに間違い。爺の作成したFlashで確認してもらえばわかるが、6番目に集めた場合は「81」、8番目に集めた場合は「79」になる。
なぜかと言うと、スタート位置が左端(1番目の旗)と定まっているからだ。問題を簡略化して旗が3本の場合を考えよう。
真ん中の2番目に集めた場合、移動距離は3メートルだが、3番目では4メートル、そして、1番目に旗を集めた場合は、6メートルになる。
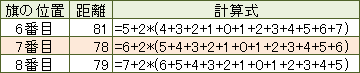
マス北野は、直観とひらめきで、わずか5秒ほどで答えを書いた。マス北野の考え方は、こうだ。直感的に真ん中の7番目に集めるのがよさそうだ。そこで、移動距離を考えると下の図のようになる。

旗が13本ということは、両端を結ぶ距離は12メートル。遠い旗から順番に真ん中に集めると、次は11、10……と距離は1メートルずつ縮まる。逆に考えると、1~12までをすべて足した数が距離「78メートル」になる。非常に明確で、じつにすっきりしている。また、旗の数が増えたとしても、1から(旗の数-1)の数を足せば、そうなるんじゃないかと。はたして、そうだろうか。たとえば、旗の数が奇数ではなく、偶数の場合だ。
マス北野の考え方では、旗が4本の場合は、1+2+3=6になるが、実際に動かしてみると、そうならないことがわかる。爺の勘違い。実際に動かしてみても、ちゃんと6メートルになる。(8月31日:修正)
東大理三の「秒殺シスターズ」の衛藤樹、伊藤理恵は、今回の問題も秒殺で解いてしまうかと思われたが、マス北野に先を越されてしまった。
まず、旗を集める位置を「x」とおくと、距離は、
(x-1)+2{|x-2|+|x-3|+……+|x-13|}
この距離が最小となる「x」を求める。
x=7のとき、
6+2{5+4+3+2+1+0+1+2+3+4+5+6}=78
結局、式にいろいろな数を代入して求めたようだ。
竹内薫センセの「美しき数学の時間」の板書きをまる写し……。

というわけで、コマ大フィールズ賞は、マス北野&ポヌさんが獲得した。平方完成に関しては、Wikipediaの二次方程式の項を見てね。
蝉の声が夏の終わりを惜しむよう。もうすぐ秋が訪れ「冷やし中華」もメニューから消える季節に……、
 たけしのコマ大数学科DVD1 (第1期) |
 たけしのコマ大数学科DVD2 (第2期) |
※コマネチ大学数学科の「過去問題」はこちらから。
■コマネチ大学数学科:2006年度全講義リスト
■コマネチ大学数学科:2007年度全講義リスト

今回は特に直観のもつ弱点がよく現れた問題だと思います。
真ん中の旗に集めればよいことはわかるのですが、それを厳密に示すには竹内先生の解法がベストでしょう。実際、マス北野や東大生の解法だったら、試験では大幅に減点をくらいます。
一般化してみますと、
全旗の数がk枚、n番目の旗に集めるときの移動距離は
(n-1)+2(1+2+…+(n-2)+2(1+2+…+(k-n))
=2n^2-(2k+3)n+k^2+k+1
=2(n-(2k+3)/4)^2+(4k^2-4k-1)/8
よって、nが(2k+3)/4に最も近い整数のとき距離が最小。
kが奇数のときは真ん中の旗
kが偶数のときは真ん中より右(スタートから遠いほう)となります。
たけしのコマ大数学科#103
たけしのコマ大数学科#103
(旧名称・たけしのコマネチ大学数学科)
フジテレビ 2008年8月28日 深夜OA
今回のテーマは、
「フラッグ」
(※この記事では回数が103になっているが、
番組的にはSPをカウントしていないので、101回目であ…