「連分数なんてこわくない」と言っている時点で、「連分数」に苦手意識を持っているのが、みえみえだ><; 「コマネチ大学数学科」でも、過去に2回ほど「連分数」という言葉が登場した。「第20講:ラマヌジャン」と「第91講:ペル方程式」だ。爺には数学の素養がなく「連分数」なんて、教えてもらったことがなかったので、「わけがワカラヌジャン!」だった。しかし「連分数」そのものは、意外と簡単な仕組みのようだ。
「数論入門」(芹沢正三/著)という本に「連分数とは」という、わかりやすい解説が載っていた。
人間は、その昔「ひとつ、ふたつ、みっつ…」と数える自然数に始まり、「負の概念」や「ゼロの概念」を加え、自然数を拡張して「整数」を作った。さらに「分数」や「小数」と、数の概念は、どんどん拡張していく。しかし、「無理数」の発見は、ピタゴラス学派を悩ましたそうな。なにせ、今までは「万物は数(自然数)である」と主張していたんだからね。
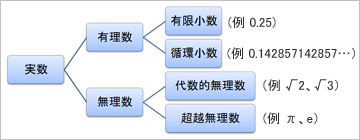
分数「1/2」なら「0.5」と小数で表すことができる。でも、「1/3」は、小数で表すと「0.333333…」といつまでも続くし、「1/7」は「0.142857142857…」と同じ繰り返しが出てきて、これが永遠に続く。「0.5」は「有限小数」と呼び、「0.333333…」や「0.142857142857…」は「循環小数」と呼ぶ。
「無理数」とは、「√2」や「√3」のように、整数の分数で表すことのできない数だ。これを「代数的無理数」と呼び、「円周率(π)」や「自然対数の底(e)」は、「超越無理数」と、ちょっと格上の呼び名がある。
で「連分数」とは、そんな分数で表すことのできない「無理数」をなんとか「分数」で表すことができないかという無謀な試み?
「連分数」の仕組みは、こうだ。たとえば「√2」の場合、小数で表すと「1.414213562」。整数部と小数部に分け、「1+0.414213562」のようにする。この少数部の逆数を求める(1÷0.414213562=2.414213562)。さらにこれを整数部と小数部に分け……以下、繰り返し。
「2、√、=、-、1、=、MS、1、÷、MR、=、-、2、=」の順序でキーを押していく。以下、繰り返し。
この取り出した整数部だけを書きとめていくと、
[1, 2, 2, 2, 2…]のようになるのがわかると思う。
これを元の小数に戻すには、
1+(1/(2+(1/(2+(1/(2+2)))))のようにする。
結果は、ずいぶん、大雑把な数値となるが、繰り返しの回数を(無限まで)増やしていけば、「√2」を表わすことができるはずだ。
仕組みがわかったところで、やはり「電卓」だとキビシイので、「Maxima」で検証しておこう。

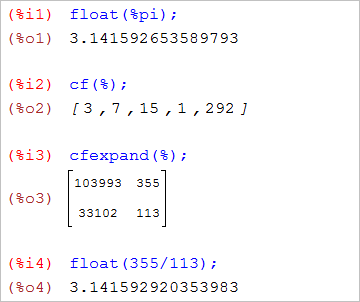
ちなみに「√3」を連分数展開すると、

「Maxima」のコマンド「cf」は、「countinud fraction(連分数)」の略で、「cflength」は、繰り返しをどこまで表示するか指定している。
ここで、根本的な疑問を感じるだろう。「無理数」を連分数展開するにあたり、「√2」を「1.414213562」と小数表現した時点で、それに続くであろう数値を切り捨て、「有限化」している。いわば、計算精度の問題になっている。実際に、有限化した際の誤差が積み重なると、正しく連分数展開はできない。たとえば「√5」を連分数展開すると[2, 4, 4, 4, 4,…」となるはずだが、途中から誤差により、乱れてしまう。
爺は「算数」脳だから、「無理数」を有限化してでも、実際に計算してみて納得したが、「数学」では、そんなことはしない。
たとえば、√3の連分数展開は……。
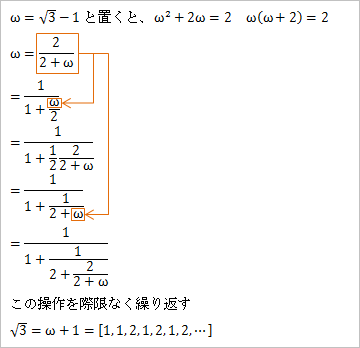
重要なのは、そのパターン、法則性が大事。「√2」を連分数展開すると「1, 2, 2, 2, 2…」となる。「√3」を連分数展開すると「1, 1, 2, 1, 2, 1, 2, 1, 2…」になる。この繰り返しが循環することを表すために、

と書く。平方根を連分数展開すると、必ず、循環型の連分数になるようだ。

自然対数の底(e)、ネイピア数を連分数展開しても、循環はしないが、そこには、ある法則があるように思える。
円周率(π)には、これといった法則が見られない。しかし、正則連分数(各部分の分子が「1」)の場合で、分子が「1」であることにこだわらないと、非常に規則正しい連分数になる。

※図版修正(2010年10月3日)
いずれにしろ、酔っ払いの「いいちこ」爺には、このへんが限界だ。
 数論入門 証明を理解しながら学べる 芹沢正三/著 講談社ブルーバックス 1595 価格:1040円(税別) |

こんばんわ。
もうすぐ(24日23:30~)「物理学」の回がはじまるところです。
「数論入門」読まれたんですね。
整数論になれていない私は、「オモロー!」ならぬ「モジュロー!(mod)」に悪戦苦闘です。(^^;
でも、整数問題ゆえに、問題自体が理解できるので、なかなかいい本だと思います。
大学入試の整数問題は、このあたりの背景を題材として出されているものが多いようですね。Webで検索すると結構情報がみつかるので、この本の内容とそちらと見比べたりするのも面白いと思います。
なにわっちさんから、ブルーバックスで「数論入門」が刊行されていることを教えてもらいましたが、同時に、小島寛之センセのブログでも「オススメ」として紹介されていたので、芹沢正三氏の「数論入門」と「素数入門」を合わせてアマゾンで取り寄せました^^;
「数論入門」を読んだと言っても、わからないことだらけです。本書は全7章で構成されており、「連分数」については、そのうちの、ひとつの章で解説しています。ですから、「書籍:数論入門」という記事タイトルをつけることはできなかったわけです。
私の場合、自分自身がつまずいたことや、なんとなく興味を持ったことが、ひっかかっていて、それが、ずっとあとになって、たまたま読んだ本にそのことが書いてあったりすると「なるほど~」と思うことが多いんですよね。興味を抱く対象というのは、まちまちで、まったくわからないことに対しては興味の抱きようもないですからね。
基礎ができてない上に、こんな感じなので、ちゃんと学習できているのかどうかも疑問です。今回の「連分数」にしても、「Maxima」だと、簡単に表示できるわけですが、どういう仕組みなのか、漠然としていたんですよね。でも、自分で計算して表示してみると、その仕組みが理解できる。まぁ、まったく興味のない人には、どうでもいいことですし、すでに知っている人から見れば「なにを今さら、当たり前のことを…」と思われるかもしれません。でも、自分が楽しければ、おもしろがることができければ、それでいいのかな、と開き直っています。
http://f.hatena.ne.jp/mathnb/20100528021239
この 廣大の函数fが ◆ いい加減法 (と命名します);
x^2=7
3倍し;3x^2=3*7
8*xを(いい加減)加え
3x^2+8*x=3*7+8*x
x*(3*x+8)=8*x+21
から 生まれた。なんて 信じる 学習者は 世界に 存在しない。
授業で いい加減法で 導出される方 は 存在しそう(嗚呼)……◆
★★ 廣大の函数f の導出過程を ご教示ください★★
(f の 導出にこそ 意味が在ると 考えます ので)
———————————————————————
また
http://f.hatena.ne.jp/mathnb/20100528021239
に倣い 例えば
Sqrt[3], Sqrt[109], Sqrt[263], Sqrt[431], Sqrt[601],
Sqrt[773], Sqrt[971], Sqrt[1153]
等のそれぞれについて
廣大の函数f に相当する函数の導出を、 遊び心で、お願い致します;
f(Sqrt[3])=Sqrt[3](不動点) f[x]=
f(Sqrt[109])=Sqrt[109](不動点) f[x]=
gbさん、コメントありがとうございます。
問題:f(x)=(8*x+21)/(3*x+8)とおく。
問(1):f(√7)=√7であることを示せ。
f(x)=√7と仮定する。
(8*x+21)/(3*x+8)=√7
両辺を二乗して、
(8*x+21)^2/(3*x+8)^2=7
(64*x^2+336*x+441)/(9*x^2+48*x+64)=7
両辺に(9*x^2+48*x+64)を掛ける
64*x^2+336*x+441=7*(9*x^2+48*x+64)
64*x^2+336*x+441=63*x^2+336*x+448
移項して
(64*x^2-63*x^2)+(336*x-336*x)=448-441
x^2=7
x=√7
よって、x=√7のとき、
f(√7)=√7は、成り立つ。
こんな答えで、点をもらえるでしょうか。
あとの問題は、かんべんしてください><;
遅いかもしれませんが、助け舟??
#陸に上がったりして><
(1)は x=√7 を代入してください。
それで一発。
(2)は、f(x)が x≧0で
増加関数だということが示せますので、
f(0)>2より、OKです。
(3)は、まず、相加相乗を考えてみてください。
x=yのとき 右辺=左辺ですから、
ルートが解けますね。
このときに、問題の左辺と、ルートを解いた後の相乗平均を比べてみてください。
50分の1 してありますからね。
そこも注意して。
(4)は、(3)と一緒です。
相加相乗で、=になるところを一つあげればいい。それだけのことです。
難しく難しく考えるより、いかに簡単に考えるか(!)。数学って言うのは、案外そういう学問です。
#もともと、理論的に筋道を立て、きちんと進める学問ですから。
#最初から難しく考えたり、公式を叩き込んだりするのはよくありません。
多分ダイジョウブだと思うけれど、
間違いがあれば、フォローお願いします。
m(_ _)m
PS.代数学屋ですので、抽象的で申し訳ない。
スイマセン、連投になりますが。
導出の過程??
出題者が作ったので、そうなるように作ったとしか言いようがありません。
問題作ったのが私ではありませんから、分からないとしか言いようがありません。
これは私作ったけど、
x^y+y^z=z^x
を満たす、整数(x,y,z)を示せ。
これだと、0^0を知っているかどうか知るために、この式を作りましたといえますけどね。
もう一個あるのか~~。
√3 でいいのかな?
適当。以上♪ 本当にそんな感じですよ。
f(x)=(x^2+x-3)/(x^2-2)
そうなるように作ればいいから、別段変な風に考える必要はないですよ。
上にも書いてますが、自分作っている問題ではないですから、何をさせたいかってのは分かりません。
f(x)が何がしかできた。
その性質が面白くなった! よし問題にしよう! かも知れないんだよ?
問題が何をさせたいか?
その問題から、何を知っているのか知らないのか?を見たいのか。
それを見つけられれば、受験生なら部分点は取れるかもしれない。
何故この式を作ったのか?
それは作った人間にしか分からないよ。
一つ上の僕の問題、東工大で実際に使われた。
頼まれたの。「数学の基礎ができているかどうか知りたい」という話をもらって。
自然数解は一個しかない。0が入ると無限にあるけど。
効果相乗平均なんかを見たかったんじゃないかな? 広大の問題は。
式の導出と何をさせたいかは、別の話ですよ。
後先が逆です。
「何をさせたいか」から「式がでてくる」
これ間違えないでね。
さきもり@福岡さん、フォローありがとうございます。
酒盛り@ガスコン研究所より。
連分数の情報を探していてこのページにたどり着いたのですが,
円周率の連分数式の左辺は π でなくて 4/π ですね.
「通りすがり」さま、間違いの指摘ありがとうございます。
記事中の図版を修正しました。