「エクセル」本の仕事が一段落して、やっと解放されたというのに、「ブログ」に「エクセル」の記事を書いている私は、どうかしているのかも><;
というのは、過去記事「■Excel2007:計算ミス」を思い出してしまったからだ。
2007年10月3日の記事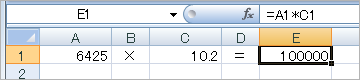
現時点(2008年5月27日)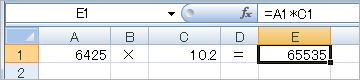
当時のコメントにも書いたけれど、
> いつのまにか自動更新のアップデートで直しちゃうんだろうな。
本当に「いつのまにか」直っている^^;
で、気になったので「エクセル」の計算精度を確認してみた。参考にしたというか、計算式を、まんま引用させてもらったのは、casioが運営している「高精度計算サイト」。さすが「♪答えいっぱつ♪」のカシオさん、スゴイっす。なんか、カタカナで表記すると「スガシカオ」みたいだけど(似てない、似てない><;)、とにかく世の中に役立つサイトで、コーポレートイメージも高まり、カシオさんの株も急上昇だ(実際の株価は知らないけれど)。
爺の世迷いごとはこれくらいにして、さっそく検証結果(2008年5月27日時点)。
●小数計算(0.4-0.3-0.1=0)
・Excel2003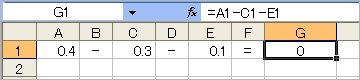
・Excel2007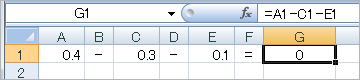
casioのサイトでは、「Excelは内部2進計算のため
2進10進変換で誤差が発生する」とあるが、Excel2003、Excel2007ともに正しい答えを出した。
●π計算(sin(9π)=0)
・Excel2003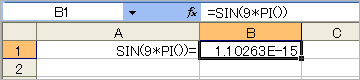
・Excel2007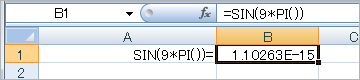
無理数(π)を有限な数値に変換するときに誤差が出るわけね、なるほど。
●無理数計算(9√2-√162=0)
・Excel2003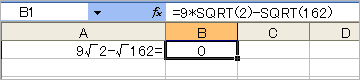
・Excel2007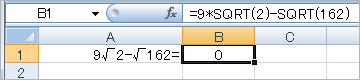
無理数を有限な数値に変換するのは同じだが、こちらは、ちゃんと計算できた(casioのサイトでは、できないことになっている)。
●複素数計算((1+i)^4=-4)
・Excel2003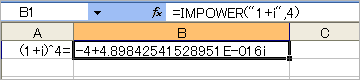
・Excel2007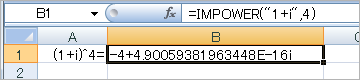
複素数のべき乗を求める関数が「IMPOWER」。「Excel2003」では、アドインの「分析ツール」を組み込む必要がある。「Excel2003」と「Excel2007」で計算結果が異なった。
●指数計算(√(1+1.23456E-100)-1=6.1728E-101)
・Excel2003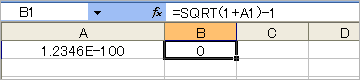
・Excel2007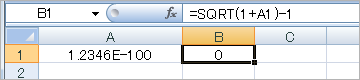
「エクセル」では、小数点以下、「0」が99個も並ぶような数の計算は正しく行えないということ。
●自然対数の底(e)のべき乗計算(e^ln(1+1.23456E-14)-1=1.23456E-14)
・Excel2003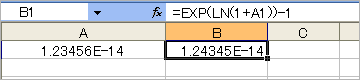
・Excel2007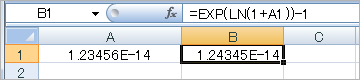
一見、正しく計算されているように見えるけれど、数字の並びを注意深く見てみると……^^;
●自然対数の底(e)のべき乗計算(e^ln(1+1.23456E-15)-1=1.23456E-15)
・Excel2003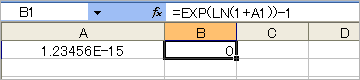
・Excel2007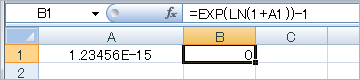
小数点以下の(0)の数をひとつ追加すると……。「エクセル」では、まったく対応できない;;
●人間の運動エネルギー(E=mc^2(1-√(1-^2/c^2)=4190.55)
・Excel2003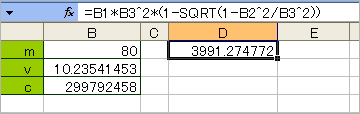
・Excel2007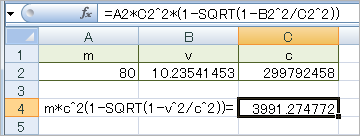
言うまでもなく、(m)は質量で、(c)は光速度。体重80kg(厳密には質量と体重は違うけれど^^)の人が毎秒(100/9.77)メートル進んだときのエネルギー量は……^^; 「ニュートン」が妻夫木聡の「ガス・パ・チョ」のCMみたいに現代に現れて、「エクセル」を使ったら、どんなコメントを残すのだろうか。

エクセルマクロ VBEの起動
エクセルマクロの編集では、VBEを使います。VBEの起動は、「開発タブ」表示からコード欄の[visual basic]ボタンをクリックします。この時点では、マクロは表示されていませんので、左側にあるプロジェクトエクスプローラーを使います。マクロは標準モジュールの下位層にあります。モジュール1を選択した場合、反転表示になります。あとはコードの表示ボタンを押せば、マクロのコードウインドウが表示されます。…