マス北野が、2008年度の「日本数学会賞出版賞」を授賞した。「テレビメディアを通じ、数学の魅力や美しさを娯楽性を兼ね備えた形でわかりやすく伝え、数学の普及に貢献した」というのが授賞理由。そんなめでたい「たけしのコマネチ大学数学科」第84講。今回は、木村美紀さん、松江由紀子さんの「卒業試験」でもある。
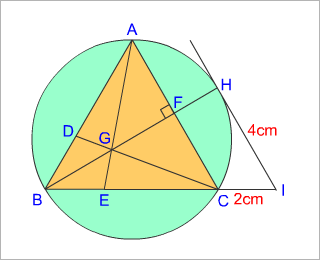
問題:BE:EC=1:2 AG:GE=3:1 BH⊥AC
HIは円の接線で、HI=4cm CI=2cm のとき、
三角形ABCの面積を求めなさい。
(※問題作成/酒井 諒さん)
今回、初めて番組視聴者からの投稿問題だ。昔、神社に奉納した算額みたく「コマネチ大学の問題」として採用され、世に知れ渡るとしたら、大変な名誉だろう。中村亨センセによると、「酒井くんの問題は、これまでのコマネチ大学で登場した、さまざまな定理を使った、とても高校1年生が考えたとは思えない、優れた問題」だと言う。
春は別れと出会いの季節。2年間、「コマネチ大学」で、さまざまな問題に取り組んだ、木村美紀さんと松江由紀子さんの「卒業試験」ともなった。コマ大数学研究会の面々もスタジオで問題に取り組むが、いつもの時間をかけ、身体を張った検証ではないので、はやくもギブアップの体。
さすがに東大生チームは、速攻で答えを見つける。いっぽう、マス北野とポヌさんは、制限時間をフルに使い、答えを出した。マス北野&ポヌさんの答えは「9√3」。マス北野の弁によると「チェバの定理とか、いろいろあるけれど、すべて、三角形の相似を使い、答えを導き出したという。中村亨センセの、するどいツッコミでは、「BHが円の直径ならば」ということ。そのへんの証明がマス北野の答えでは、あやしい。東大生チームの答えも「9√3」だが、「メネラウスの定理」、「チェバの定理」、「円周角の定理」などを使い答えを求めた。
ここで、新入生の答えが紹介された。「現役東大理科三類チーム」の衛藤 樹さん、伊藤理恵さんの答えも「9√3」。「現役東大生青春ド真ん中チーム」の小橋りささん、生駒尚子さんの答えも「9√3」。
中村亨センセの「美しき数学の時間」で、美しく締めてもらおう。
というわけで、感覚的に三角形ABCが正三角形とわかれば、面積を求めることは、「方べきの定理」で、すぐ求めることができるけれど、三角形ABCが正三角形であるという証明に、「メネラウスの定理」や「チェバの定理」、「円周角の定理」、「接弦定理」などが必要になるんだね。
最後に「コマ大生」は、新入生のスケッチを描いて紹介していたので、私も「コマ大数学研究会」の一員として、新入生のスケッチを描いてみた。あくまで、爺のフィルターを通して見た印象なので、ツッコミは入れないように^^;
 
|
酔っ払い爺の第1印象は、熟女フェロモン?親分肌の、伊藤理恵さん、清楚な佇みだが芯が強い衛藤 樹さん、笑顔が眩しいが、声が低音、笑顔とは対象的に声が冷めている、生駒尚子さん、ちょっとオトボケな、その天然キャラに期待の小橋りささん。
いずれも、一見しただけで、強烈な個性のオーラを発する新メンバー。これは、新学期がおもしろくなりそうだ^^;
≪参照≫
■日本数学会ホームページ
≪今回制作したFlashのダウンロード≫
comaneci84.zip

メネラウスの定理
CB/BE*EG/GA*AF/FC=1
を用いればAF=FCがいえるので
チェバの定理は不要では?
コマネチ大学 #83
コマネチ大学 #83
たけしのコマネチ大学数学科#83 2008年3月20日 深夜OA
今回のテーマは、
「卒業試験」
【New!! DVD】
たけしのコマ大数学 科
DVDBOX 1
¥5,284
【定番本】
コマ大数学科
特別集中講座
ビートたけし
¥1,000…
その通りですね、ヌルハチさん。
気が付きませんでした。
今回は惨敗でした。問題の図の様子から「10平方センチメートル」ぐらいと勘で思いましたが、計算が全く出来ませんでした。
しかし、東大生の解説の「方べきの定理」と聴いた瞬間、半分ほど解けました。そのあと時間をかけて考えたら解けました。
解説では「千葉真一の定理」…もとい「チェバの定理」や「メネラウスの定理」などを使っていますが、それらの定理を知らなくても解けます。おそらくマス北野式の解答と同じだと思います。実は私これら2つの定理、名前は聞いたことはありますが、内容は覚えていません。
何はともあれ、木村さん松江さんお疲れ様でした。次回からは東大生組が2組登場なのでしょうか?マス北野はいよいよ苦戦するでしょう。
ヌルハチさん、ピョンキチさん、藤崎さん
コメントありがとうございます。
「コマネチ大学数学科」は、しばらく春休みのようですね。この間に、私は「ガスコン研究所」の活動資金と酒代を得るため、精を出さねば^^; 更新が滞ると思いますが、今後ともよろしくお願いいたします。
コメントが今さらで申し訳ないのですが、
AF=FCの時点でBHは直径と分かるのではないでしょうか。
そうすれば円周角の定理以降は不要で、三角形の相似で求められるのではないでしょうか。
私も録画をいまさらみてコメントなのですが、確かに皆さんのいうように条件が多いですね。
AEやCDの直線はなくても(チェバやメネラウスの定理は不要)ABCは正三角形に決まります。
以下参考まで。
AC⊥BHなのでBHは直径。
∴∠BCH=90°。
⊿HCIは1:2:√3の直角三角形なので、∠I=60°。
HI//FCなので∠C=60°。
∠BHC=90°-∠IHC=60°。
円周角は等しいので、∠A=∠BHC=60°
∠A、∠C共に60°なので⊿ABCは正三角形。
難しい図形問題を作ろうとするとよく起こることですが、高1にしてはよくできた問題ですね。
(∠AFB=90°が無ければ最高)
最後に、似顔絵がかなり上手で驚きました。
ぶりちゃん、ちーかまさん、コメントありがとうございます。
数学落ちこぼれの爺にとって、なにが苦手かと言うと、「証明問題」なのですよね。どんな手法を使っても、証明できるなら、それで、いいじゃん! と思ってしまうのです。
でも、数学を愛する人は、もっとスマートな証明方法があるじゃん! と思うのでしょうね^^;