■書籍：数学流生き方の再発見

　秋山仁センセの著書「数学流生き方の再発見」からの配線問題。

問題：平面な基盤上に「＋端子」、「－端子」がそれぞれ10個ある。これら20個の端子から、どの3個の端子を選び出しても一直線上にないとするとき、ショートしない（端子どうしを結んだ線が交差しない）ように配線せよ。

【遊び方】「Reset」ボタンを押すと、勝手に「＋端子」と「－端子」を配線するが、いいかげんな爺が作ったFlashでは、線が交差してショートしてしまう。そこで、「Play」ボタンをクリックして、交差しないような配線の仕方が必ずあることを証明してほしい。配線は、「＋端子」をドラッグして、「－端子」でドロップする。画面下の数値は、配線の長さ。左側が爺のスコアで、あなたは、配線をショートさせることなく、爺のスコアよりも、配線の長さを短くし、少ないスコアを目指してほしい。

　「どの三点も同一直線上に並ばない」という条件は、幾何学で「一般の位置」と言うらしい。いいかげんな爺のFlashでは、X軸上、Y軸上で端子が並ばないように留意したが、斜めに三点が一直線上に並んでしまうかもしれず、厳密に条件を満たしていないことを断っておく。（いいかげんさ、爆発＞＜；）

　端子どうしを結ぶ配線が交差してもよいとすると、10の階乗(362万8800)通りの結び方がある。その中には、配線の長さの総和が最も小さくなる結び方が存在する。問題を簡略化して、[+]端子2個、[-]端子2個の場合を考えてみよう。

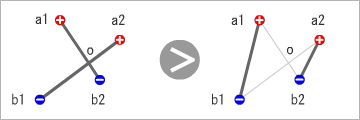
　三角形(a1, o, b1)と(a2, o, b2)を考えると、「♪三角形の二辺の和、他の一辺より長い♪」で交差しないほうが、配線の長さが短くなることは、わかってもらえると思う。

　秋山仁センセの「数学流生き方の再発見」では、背理法を用いて証明している。つまり、この問題の答えは、はっきりしている。最短の配線をするならば、配線はショート(交差)しない。端子の数を「n」とした場合でも、問題の条件を満たしていれば、必ず、交差しない配線の仕方がある……ということだ。秋山仁センセは「この事実は大変、美しいものと映る」と述べている。

　「端子の数がnのとき、必ず交差しない配線の方法があることを証明しなさい」(条件は同じ)。という問題が数学オリンピックで出されたとき、この証明問題をあっさりと解いてしまった15歳の少年がいたそうな。

「数学流生き方の再発見」より引用/*
大人の質問「キミはどうして、線分の長さの総和が最小な結び方に注目したのか？」
少年の答え「オジさん、そんなの当たり前だよ、電線の長さ(線分の長さの総和)が長ければ、長いほど、どっかでクロスして、ショートしやすくなるからさ」
*/引用終わり

　いやはや、なんとも小憎らしい少年だなぁ＾＾；　会話のディテールはともかくとして、秋山仁センセが書いているのだから、こんなやりとりが実際にあったのだと思う。

　この「配線問題」は、「サラリーマン巡回」の問題と同じく、nが10個くらいだと、人間は直感的に解決できるけれど、nが１万個とか、100万個になると、人間の直感では無理だし、すべての解を調べつくす方法では、コンピュータに解かせることも難しい。大規模集積回路などの設計では、できるだけコンパクトに配線も短くし、最適化をはかる必要があるけれど、「配線問題」は、なかなか難しい問題のようだ。問題解決のひとつの方法として「コマネチ大学数学科77講」で紹介した「ラグランジュの未定乗数法」が使われることがあるらしい。難しすぎて、爺には、さっぱり、わからないことは、すぐに証明できる＾＾；

　本書の第一部は「寅さんは難関大学に合格できるか」という章タイトルで、もしもフーテンの寅さんだったら、数学の問題をどう解くか？　寅さんの数学的能力を斬る……という、おもしろい語り口になっている。その一例として、「コマネチ大学数学科79講：ハミルトン」の記事で、本書に掲載している問題を紹介したが、他にも過去「たけしのコマネチ大学数学科」で紹介された問題が掲載されているよ。どんな問題なのかは、過去記事を参照してほしい。

■第5回：ケプラー予想（コイン詰め問題）
■第9回：美術館定理
■第23回：繰り込み（トランプ夢の架け橋問題）

数学流生き方の再発見 ―数学嫌いに贈る応援歌 秋山 仁／著 中公新書 680円＋税 ISBN4-12-100986-X

---