今回の「たけしのコマネチ大学数学科」は、「男女7人物語」ではなく、なんと、男20人女20人、あわせて「男女40人問題」。合コンレベルではなく、お見合いパーティーのような感じだが、カップルを誕生させるのではなく、男女別に並び替える問題だ。
問題:交互に並んだ40人の男女を男女別に20人ずつに並び替えるには、最低何回の移動が必要か。移動は隣り合った2人を同時に行う。移動中に順序を入れ替えることはできない。また、途中に空きがあってはならず、男20人、女20人が連続して並んでなければならない。

【遊び方】クリックすると、別窓で開くはず。キーボードの上下左右の方向キーを使う。キーを押しても動かないときは画面内を一度クリックする。上がり判定はチェックしていない^^;
いきなり男女40人を並び替えるのは大変。番組では中村亨センセによる「男4人女4人」の場合の移動方法が紹介された。そこで少ない人数から始め、なにか法則があるかどうかを検証してみよう。
何度か遊んでみれば、男4人女4人の場合は、4手で済むことがわかる。
コマ大数学研究会は、芸能人カップル20組の、それぞれ男女の名前を書いた札を並び替えて検証。ロケ時の検証では22回だったが、スタジオでは、それより少ない20手で並び替えることができた。

マス北野は、男4人女4人の問題の答えが4手なので、全体を5組に分け、右から1組ずつ、残りの組は無視して、動かしていけば、4手×5組で20手になるという答え。

しかし、マス北野の方法では、上の図のような結果になり、さらに並び替えが必要になる。木村美紀さん、松江由紀子さんの東大生チームは、4手×5組で20手にプラスして、さらに13手の並び替えが必要として、20+13で33手という答えになった。

実際に動かしてみると、13手もかからないようだ。
さて、中村亨センセの「美しき数学の時間」。男8人女8人の場合で考えると、下の図のように2手進めたところで、図の緑の部分に注目すると、男4人女4人のパターンと同じだ。この部分の移動は4手であることがわかっている。すると、残り2手で並び替えが完了する。
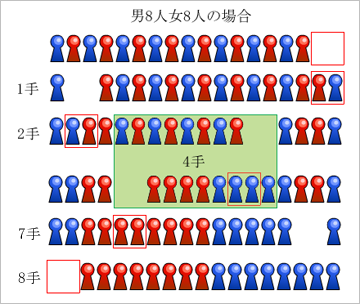
つまり、男8人女8人の場合は(2手+(男4人女4人の手数=4)+2手)で8手。男12人女12の場合は(2+(2+(4)+2)+2)という具合に入れ子状態になり、最終的に男20人女20人の場合は、20手で並び替えが完了する。
男女1人ずつのペアを「n」とすると、
a(n)=a(n-4)+4
という漸化式になる。(※追記:ただし、n≧4)
たとえば、男20人女20人の場合を、この漸化式に入れると、
a(20)=a(20-4)+4=20
という具合だ。
最初に男4人女4人の場合で考えたが、男5人女5人なら5手、男6人女6人なら6手で解けるということだ。ホントに解けるかどうか確かめてみよう^^;
≪今回、制作したFlashのダウンロード≫
comaneci78.zip(※Flash8)
※追記:重要なことを書き忘れていた。コマ大数学研究会が2週連続して、コマネチ・フィールズ賞を獲得したことだ。「数学は体力だ!」コマ大ファイト、ファイト、ファイト!

コマネチ大学 #77
コマネチ大学 #77
たけしのコマネチ大学数学科#77 2008年2月07日 深夜OA
今回のテーマは、
「おしどり問題」
【定番本】
コマ大数学科
特別集中講座
ビートたけし
¥1,000
【New】
逆転発想力パズル
脳が目覚める
竹内薫 中村亨…
「夜中に犬に起こった奇妙な事件」、読みました! いい本ですね。
ところで、私のブログからリンクを張ってしまいましたが、大丈夫でしょうか?
竹内センセ
コマネチ人としての紹介(リンク)ありがとうございます^^;
今,アメリカで勉強中ですが,こちらでもインターネット契約で,日本の番組を見ています。おかげで,コマネチ大学数学科がこちらの水曜日のお昼頃に見ています。それから,録画も。高校の数学の教員をしてて,進学指導の数学のほかに,2年生で,何か「考える経験を」数学の苦手な生徒にさせる方法を模索しているところです。少し,ヒントが見えてきているのですが,その中で,たけしのコマネチ大学で扱っている内容が参考になっています。今日は,今日,Gasconさんのブログで,とても詳細にしかも,フラッシュで,試行錯誤しながらできるし,しかも,フラッシュのプログラムのダウンロードまで許可してくださってて,感動しています。この夏に帰国し,職場にもどるのですが,それまでに,これまでと少し違う,でも,生徒の進学指導も徹底しながら,数学を楽しむことを経験させられる授業を作って帰国したいと思っていました。これからも,参考にさせてください。今日は,とても感動しました。長いコメントになりましたが。毎週,楽しみにしています。
あさとみかさん、コメントありがとうございます。
私は学生時代「数学」の授業はちっとも面白くなかったのですが、爺になってから数学の入門書などを読むようになり、「数学」を楽しむ余裕が少し生まれました^^;小島寛之センセの言葉を借りるなら、「数学」下手でも、「数学」嫌いになる必要はない。下手の横好きでいいんだということですね。
もっとも、学生時代に「数学」好きになれば、「好きこそものの上手なれ」で、少しは「数学」上手になれたのかなぁ……と思うこともありますが、それを言っちゃあ、おしまいよ、ですね。なんだか、爺になると、覚えることよりも、忘れることのほうが多いように感じるもので^^;
いずれにしろ学生時代に「数学を楽しむことを経験させられる授業」を受けることができる生徒さんたちは幸せだと思います。
おしどり問題
男女男女男女男女空空
の隣り合う二人を空席移動して、
男男男男女女女女空空
女女女女男男男男空空
空空男男男男女女女女
空空女女女女…
僕はこの問題を円を想像して解きました。紙とペンが手元に無かったので、頭の中でですが…まず、頭の中で男女40人交互の円を想像して、20人20人の上下半分に円を分けました。20人20人の偶数同士なので、円の直径は異性のはずです。で、上、男10人女10人、下、男10人女10人なので、片方から男10人、片方から女10人を交換した20手だと考えました。