「ラグランジュ」と言って思いつくのは、地球と月との間の引力がゼロになる「ラグランジュ・ポイント」くらい。でも、この「ラグランジュ」かなり便利なものらしい「たけしのコマネチ大学数学科77講」。
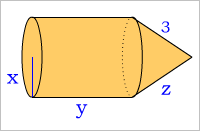
問題:図のような円柱と円錐を組み合わせた「エンピツ型」の立体がある。円錐の母線(底面の外周の任意の点と頂点を結ぶ線)は「3」である。この立体の体積が一定としたとき、最小の表面積になるような、底面の円の半径「X」を求めよ。
※スライドバーをドラッグして「X」の値を変更し、表面積を最小にする。
コマ大数学研究会は、それぞれが、同じ量の粘土で自分が最小の表面積になると思う「エンピツ型」の立体を作る。細長いものから、寸胴のように太いものまで、さまざま。出来上がった立体の表面に紙を貼り付け、その紙の面積が一番少なかったものを解答とする。
今回の問題のポイントは、一定の体積というだけで、その値がわからないこと。体積がわからなくても、一定という条件だけで答えが出るらしいのだが、それだと難しいので、竹内薫センセから、体積は「61.3」というヒントが出る。
マス北野とポヌさんコンビ、木村美紀さんと松江由紀子さんの東大生チームは、連立方程式を立て、それを解こうとするが、「74講のピタゴラス」の回と同じように、計算が大変なことに……。
コマ大生の答えは「2.35」、ポヌさんは、微分して「0.64」という答え。マス北野は「4.4」という答えだが、どう考えても「X」は「3」以下。東大生は、「X」の値は正(0<X<3)のあたりをつけ、いろいろな値を「X」に代入した結果、その中で最小だった「2.8」という答え。
ここで、体積と表面積の求め方を確認しておこう。
■体積
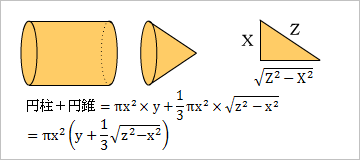
※2月10日追記:Yukiさんの指摘により、図の誤りを修正。
■表面積

竹内薫センセの「体積は61.3」というヒントを使えば、「X」だけの式にすることができる。
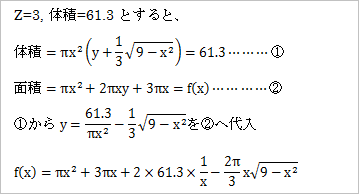
この式に「X」の値を少しづつ変化させて代入すれば、「エクセル」でグラフを描くことができる。
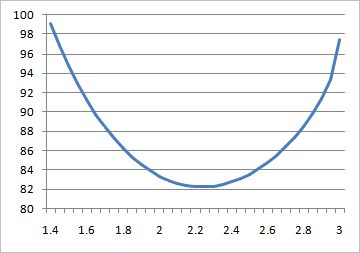
だいたい、2.2~2.3の間で表面積が最も小さくなることが視覚的にわかるよね。しかし、微分して最小の表面積のときの「X」を求めようとすると、大変なようだ。私は、未だに微分積分がよくわからないので、偏微分などと言われても偏頭痛がしてくる;; 竹内薫センセの「美しき数学の時間」によると、このように計算が大変なとき、「ラグランジュ未定乗数法」を使うと、スッキリ解けるらしい。以下は、わけがわからないまま、番組内で竹内薫センセが解説に使用したホワイトボードの丸写し^^;
■ラグランジュ未定乗数法


※2月10日追記:Yukiさんの指摘により、図の誤りを修正。
というわけで、最小の表面積になるXの値は「√5」が正解。コマ大生がもっとも近い答えだったので、コマネチ・フィールス賞を獲得した。体積がわからなくても、答えが出ちゃうというのがスゴイぞ「ラグランジュ未定乗数法」。それにしても、さっぱり、わからない;;
≪今回制作したFlashのダウンロード≫
comaneci77.zip
※Flash8が必要

こんにちは、いつも楽しく拝見させていただいています。
関西地区なので、「予習」になってますが。(笑)
ラクランジュって聞くと、ラジュランジュポイントですよね。
で、未定乗数法ってピンと来ないところは否めないですが、
これを使うと次のようなことを調べることができます。
長さが一定の輪っか(ひも)で囲むことのできる図形を考えたとき、面積が最大となるものは?
答えは「円になったとき」になります。これも未定乗数法で求められます。
これを応用していくと、運動方程式やはたまた対称性(先の円も対称性ですね)といったことが導き出されます。
数学書と紹介されていますが、物理屋さんは忘れたくても、忘れられないキーパーソンです。
(いまはIT系の仕事をしてますけど、忘れられません。笑)
コマネチ大学 #76
コマネチ大学 #76
たけしのコマネチ大学数学科#76 2008年1月31日 深夜OA
今回のテーマは、
「ラグランジュ」
【定番本】
コマ大数学科
特別集中講座
ビートたけし
¥1,000
【New】
逆転発想力パズル
脳が目覚める
竹内薫 中村亨
¥…
はじめまして、
ラグランジュの未定乗数法の板書を写しきれなかったので調べていたらgoogleでここに辿り着きました。
過去の問題も見ることができてとても助かっています。
ええと、復習をしていて何カ所か気になったのですが。
体積で
πx^2{y+(1/3)*√(x^2-z^2)}
のところは√の中のxとzが逆ではないでしょうか?
それとFをxについて微分してd/dx Fの最後の
-(1/3)λπx^2*{1/√(z^2-x^2)}
のところは最後の1/√(z^2-x^2)の分子はxで
-(1/3)λπx^2*{x/√(z^2-x^2)}
また、λの値は2/xではなく-2/xだと思うのですが。
とりあえず自分で計算していたらこうなったのですが、こちらの計算ミスなら申し訳ありませんm(__)m
なにわっちさん、コメントありがとうございます。
Yukiさん、間違いの指摘、ありがとうございます。
「ぎゃ!」思わず赤面*^^*
該当箇所を修正しておきます。