今回の「たけしのコマネチ大学数学科」は、先の「国際エミー賞」のVTRを含めた、「数学ワールドカップ」1時間特番。「国際エミー賞」に関しては、残念だったけど、2006年4月にスタートした、当番組は、2学年。マス北野の「もいっかい、行ってやろうかな」の言を信じ、来学年に期待。今回はアメリカから東大に留学中のジョナサン・ヘッドさんと、ソウル大学医学部卒業の韓国スター、ジョンフンを迎え、いつもは、マス北野とチームを組む、ポヌさん、東大生チームの木村美紀さんと、松江由紀子さん。そして、マス北野と、我らがコマ大数学研究会を含めた、個人バトルだ。
まずは、第1ROUND。マス北野が得意とする「直観、ひらめき」勝負の問題。挙手による解答順で、正解者には、20pt、15pt、10pt、5ptが与えられる。
第1問は、マス北野は一番早く挙手するも、解答は「25個」と不正解。ジョナサンさん以外は、全員不正解で、ただひとり、20ptを獲得した。
第2問もマス北野が早かった。

自分でも「きれいだね~」と自賛するのもうなづけるほど、美しい解答だ。2番手は、ジョンフン、そして3番手はコマ大生と続くが、コマ大生の解答は「最大公約数とはなんなのか? が最大の謎」と言う通り不正解^^;ジョンフン、松江由紀子さん、木村美紀さん、ポヌさんが正解した。ジョナサンさんはギブアップ。
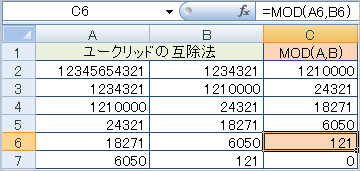
「ユークリッドの互除法」は、12345654321を123454321で割り「除数をその余りで割る」を繰り返していく。最後に余りが「0」になる場合は、その直前の余りが最大公約数となる。
2問終了時点で、マス北野とジョナサンさんが得点20ptで並ぶ。第3問も、マス北野が一番早く挙手したが、切った紙を並び替えるのに手間取っている間に、ジョンフンが挙手。戸部アナが「1番」の札をジョンフンに置き換えてしまった^^;コマ大生は、4番手で正解。
予選第1ROUNDが終了した時点での得点は以下のとおり。決勝ROUNDの第4問は、中村亨センセの「美しい解き方」を含めた、判定ポイント(100点満点)が加算される。
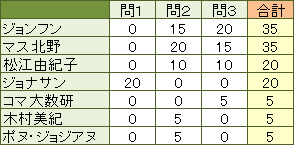
マス北野とジョンフンが35ptで並んだ。決勝ROUNDの第4問は「ハノイの塔」。ただし、通常の「ハノイの塔」と違い、AとCの棒に5段のハノイの塔があり、これをすべてBの棒に移動せよ! というもの。ルールは同じで一度に動かすことのできる円盤は1個。小さい円盤の上に大きい円盤を重ねてはいけない。ハノイの塔を完成させる、最小手数を求めよ。
【遊び方】たとえば、AからBへ移動させるには、Aのボタンをクリックしたあと、Bのボタンをクリックする。小さい円盤の上に大きい円盤を重ねてはダメというルールはチェックしていないので、自分で判断してね。
ジョンフンは、ただひとり「ハノイの塔」の模型を使わず、ひたすら鉛筆を動かす。完成形の前段階、1手前、2手前に求められる形を考え、順にそこに至る手数を数える、数学的発想だ。答えは「112手」だが、自信はないと言う。
松江由紀子さんは、円盤が数が少ないときの手数を数え上げ、それらを足し合わせる考え方。複雑な問題を理解できる単位に分解し、法則を見つける。これも数学的発想法のひとつ。答えは「91手」で、解答の中ではもっとも小さい。
マス北野は、一般的な「ハノイの塔」の手数が(2^n-1)になることを知っていた。しかし、答えは、解答の中でもっとも大きい「238手」。本人曰く、途中から江原啓之の「この数字を書け」という声が響き、従ってしまったと^^;
コマ大数学研究会は、公開ロケで検証した結果は「113手」だったが、神が舞い降りたのか、スタジオでの検証では「96手」になった。
というわけで、正解は「96手」で、コマ大数学研究会のみが正解した。
一般的な「ハノイの塔」を解く手数の一般式は、マス北野の言うとおり「2^n-1」になる。この問題の一般式は、「(40×2^n-18×n-39-(-1)^n)÷12」になるそうだ。
さて、中村亨センセの判定ポイントを加算した最終結果は……。
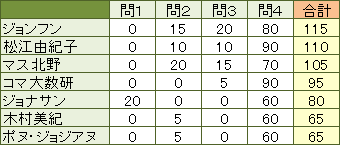
優勝は韓国スターの「ジョンフン」に決定した。しかし、私としては、コマ大生の奮闘を讃えたい。
最後に今年一年間、このブログを訪れてくれた多くの方々に感謝。よいお年を……。

今年は応援ありがとうございました!
4月にはDVDが発売される予定です。
来年もよろしくお願いいたします。
コマネチ大学2007年末SP (数学ワールドカップSP編)
コマネチ大学2007年末SP
(数学ワールドカップSP編)
たけしのコマネチ大学数学科
数学ワールドカップSP 2007/12/27 深夜OA
「マス北野現役東大生に最強刺客勝者は誰!?
数学、ワールドカップ。開幕!!」
※記事が二つに分かれています。
国際…
コマネチ大学2007年末SP (国際エミー賞舞台裏 完全密着ドキュメント編)
コマネチ大学2007年末SP
(国際エミー賞舞台裏 完全密着ドキュメント編)
たけしのコマネチ大学数学科
数学ワールドカップSP 2007/12/27 深夜OA
<第35回・国際エミー賞舞台裏 完全密着ドキュメント>
クリックすると国際エミー賞のサイトへ
※…
あけましておめでとうございます。
番組で紹介されていたのとは、別の一般式を導きました。
n段2つのハノイの塔の、最小手数をS(n)とする(nは自然数)。
S(1)=2
S(2)=7
S(≧3)=S(n-2)+1+2{2^(n-2)-1}+2(2^n-1)
=S(n-2)+10・2^(n-2)-3
どうでしょう(^^;)下の2段を無視して、残りを真ん中に集めるのにS(n-2)手。端から端へ1個動かして、そこに真ん中の塔を移すのに1+2{2^(n-2)-1}手。残りが2(2^n-1)手。整理してS(n-2)+10・2^(n-2)-3手。
ただ、こっから「(40×2^n-18×n-39-(-1)^n)÷12」を導くのは、私の素養では無理です。
先日、初書き込みをしました藤崎といいます。
このハノイの塔の問題は「2つの山を一つにまとめる回数」を求めますが、このまとめかたで回数が変わります。円盤の数をn枚としたとき
番組で出した「中央にまとめる回数」を x(n)
「左右どちらか一方にまとめる回数」を y(n)
とおくと次の関係があります。
x(n) = y(n-1)+2^(n+1)-2
y(n) = x(n-1)+2^n-1
以上から
x(n) = x(n-2)+5*2^(n-1)-3
という式が出ます。この式と x(1)=2, x(2)=7 という数(この数は実際に動かして調べる?)を使うと x(n) が計算できます…
と簡単に書きましたが、この計算はおそらく大学入試以上のレベルの問題だと思います。同じように y(n) も計算できますが x(n) の計算でもううんざりです。
謹賀新年
あけましておめでとうございます
昨年はお世話になりました。
今年もどうぞよろしくお願い致します。
あけましておめでとうございます。
竹内センセ、ともみさん、藤崎さん、シャブリさん、
コメントありがとうございます。
正月の三が日も過ぎ、お屠蘇気分でもアルマーニ、私の場合は、いつも「いいちこ」気分なので、あいかわらず酔っ払っています。
一般的なハノイの塔の手数をH(n)とすると、
H(0) = 0
H(1) = H(0)+1+H(0) = 0+1+0 = 1
H(2) = H(1)+1+H(1) = 1+1+1 = 3
H(3) = H(2)+1+H(2) = 3+1+3 = 7
H(4) = H(3)+1+H(3) = 7+1+7 = 15
H(5) = H(4)+1+H(4) = 15+1+15 = 31
≪参考≫
「プログラマの数学」結城 浩/著
というわけで、[n]段のときの手数は、ひとつ前の段の答え(n-1)を2倍して1を加えると得られます。一般式は「2^n-1」になりますよね。
「コマネチ大学数学科:ワールドカップSP」のダブルハノイの塔の一般式(閉じた式)が、なぜ「(40×2^n-18×n-39-(-1)^n)÷12」になるのか、私にも導出することができません><;
それどころか、ともみさんや、藤崎さんのように漸化式を求めることも、あきらめてしまいました;;
でも、上記の「プログラマの数学」をマネて、ダブルハノイの塔の手数をS(n)とすると、
S(0) = 0
S(1) = S(0)+2+S(0) = 0+2+0 = 2
S(2) = S(1)+2+S(1)+? = (2+2+2)+1 = 7
S(3) = S(2)+2+S(2)+? = (7+2+7)+3 = 19
S(4) = S(3)+2+S(3)+? = (19+2+19)+4 = 44
S(5) = S(4)+2+S(4)+? = (44+2+44)+6 = 96
……となり、「?」の部分は[n]が偶数のときは、1コ増え、奇数のときは2コ増えます。
「だから?」と言われても困るんですが、これも法則だと思うんですよね^^;
ちなみに、記事中、解答のFlashムービーを掲載しましたが、これは、再帰的なプログラミングで計算したものではなく、1手ごと、コツコツと自分で動かして、それをムービーにしたものです。「なぁ~んだ」という感じですね><;
だから、私は、数学落ちこぼれの爺なんだってば^^;
こんな爺ですが、本年もよろしくお願いいたします。
ハノイの塔の一般式導いてみました。
ちなみに、
①両側n枚×2を全部真ん中に集める回数をx[n]
②両側n枚×2を右か左に全部集める回数をy[n]
③ひとつの棒に2n枚あるのを他の棒に全部移す回数をz[n]
として漸化式をたてました。一応高校レベルで解けますが、非常に解きがいがあるものでした。
ちなみに答えはnが偶数の時と奇数の時で違います。番組で紹介された一般式は、(-1)^nを利用してすべてのnに対する一般式を求めたみたいです。
全く才能なしですが、なんとか漸化式を導けました。
一部、不明な点もありますが、どなたかフォローしてくれると
ありがたいです。
まずは私なりの手順の解釈です。
1.左右の上部n-2段までを中央に移動
2.右(左でもいい)のn-1段を左に重ねる
3.真ん中に集めたn-2段までを全部左に
4.右に残った最後のn段目を真ん中に移動
5.左の一番下を除いたn-1段までを全部右に移動
6.左に残った最後のn段目を真ん中に移動
7.右のn-1段すべてを真ん中に移動
で、以上を式にすると、
D(n) = D(n-2) + 1 + 2S(n-2) + 1 + 2S(n-1) + 1 + 2S(n-1)
となります。1.は即ちn-2段の2つハノイの塔の手順ってことなので、D(n-2)となります。
S(n)は通常の1つのハノイの塔n段の場合の手順数で、すでに紹介されているように、
S(n) = 2^n – 1
3.の手順は、各段が2枚ずつになったn-2段の通常のハノイの塔と考えられるので、移す手順は2*S(n-2)です。
5.7.も同様です。
で、上の式を展開すると、
D(n) = D(n-2) + 2*(2^(n-2) – 1) + 4*(2^(n-1) – 1) + 3
= D(n-2) + 2^(n-1) – 2 + 2^(n+1) – 4 + 3
= D(n-2) + 2^(n-1) + 2^(n+1) – 3 ・・・式1
となりました。
これでも十分問題を解けるのですが、漸化式を目指します。
いろいろ調べたのですが、
D(n) = (Dn-2) + f(n)
の形をズバリ解く方法は見当たらなかったので、自分流で強引に行きます。
式1をn=2..nの範囲で足すと、左辺と右辺の最初のD(n-2)の項が打ち消しあって
D(n) + D(n-1) = D(0) + D(1) + ∑(k=1..n-1 2^k) + ∑(k=3..n+1 2^k) – 3(n-1)
= 0 + 2 + [2^n -1 – 1] + [2^(n+2) – 1 -(2^0+2^1+2^2)] – 3(n-1)
= 5*2^n – 3n – 5 ・・・式2
ここで、
∑(k=0..n x^n) = (x^(n+1) – 1)/(x-1)
という公式を利用しています。kの範囲に注意して余計な項を引きます。
で、
D(n) = -D(n-1) + 5*2^n – 3n – 5
D(n-1) にマイナスが付いていなければもっと楽なのですが、この場合は両辺を
(-1)^n で割って(掛けてもこの場合は同じ)
D(n)*(-1)^n = -D(n-1)*(-1)^n + 5*2^n*(-1)^n – 3n*(-1)^n – 5*(-1)^n
d(n) = D(n)*(-1)^nとおくと、
d(n) = d(n-1) + 5*(-2)^n – 3n*(-1)^n – 5*(-1)^n
となり、式2を導いたときのように総和の公式を使って、
d(n) = d(1) + ∑(k=2..n 5*(-2)^k) – ∑(k=2..n 3n*(-1)^n – ∑(k=2..n 5*(-1)^n)
・・・式3
ここで、正直2番目の項∑(k=2..n 3n*(-1)^n) を展開する方法がわかりませんでした^^;
ただ、0,-3,3,-6,6,-9,9,… という数列になるので、これに合うように
∑(k=1..n 3n*(-1)^n) = 3n{1-(-1)^(n+1)}/4 – 3(n+1){1-(-1)^n}/4
としました。これを使って、式3は
d(n) = d(1) + [5{(-2)^(n+1) – 1}/(-2-1) – (-10) – 5]
– [3n{1-(-1)^(n+1)}/4 – 3(n+1){1-(-1)^n}/4 – 3]
– [5{(-1)^(n+1) – 1}/(-1-1) – (-5) – 3]
= …
= -5*(-2)^(n+1)/3 – 3n*(-1)^n/2 – 3*(-1)^n/4 + 5*(-1)^(n+1)/2 – 1/12
となります。これを元のD(n)に戻すために各辺に(-1)^n を掛けると、
D(n) = 5*2^(n+1)/3 – 3n/2 – (-1)^n/12 -13/4
となりました。中村センセの一般式と同じ、ですよね?
一応、5段まで検算しましたけど、あっていそうです。
あー、超疲れました。一部インチキなので、誰かわかる人フォローお願いします。。。
みのりあんさん、コメントありがとうございます。
& お疲れさまでした^^
すごいっス。