■コマネチ大学数学科66講：ピックの定理

　「ピック？子豚さん？ 私も太り過ぎないように頑張ります。ブヒッ、ブヒー！」というオープニングの戸部アナに「それは、ピッグだろ」と、ひとり、むなしくテレビ画面にツッコミをいれつつ「たけしのコマネチ大学数学科」第66講。始まり、始まりー。

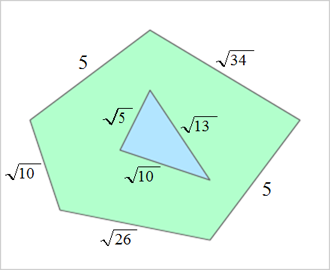
問題：碁盤の目のように等間隔に道が通っている図のような形の街がある。この街の中には交差点が37個ある（外周上にある5つの交差点は含まない。街の中央にある池の中の交差点(?)は含む）。外周の長さ、池の周囲の長さは図の通り。この街の面積(陸地のみ)を求めよ。

　問題の地図には、肝腎の交差点が描かれていない。そこで、等間隔の道(格子)を描く。すると、図のように街の地図は7×9のマス目に収まる。7×9のマス目から、街の周りの5つの三角形と1つの正方形の面積を引けば、街の面積になる。

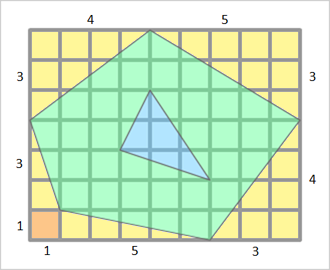
街全体=(7*9)-(3*4)/2-(5*3)/2-(4*3)/2-(5*1)/2-(3*1)/2-(1*1)=38.5

池の面積も同様に3×3のマス目から周りの3つの三角形の面積を引いて求める。

池の面積=(3*3)-(2*1)/2-(2*3)/2-(3*1)/2=3.5
街(陸地)の面積=街全体(38.5)-池(3.5)=35

　というわけで、答えは「35」

　今回はコマ大生、マス北野とポヌさんコンビ、東大生チーム、全チームが正解。皆の関心は、これを使えば秒殺で答えがわかるという「ピックの定理」に移った。

　竹内薫センセの「美しき数学の時間」によると、ゲオルグ・ピック(Georg Pick 1859-1942)は、16歳でウィーン大学に入り、20歳で博士号を取ったらしい。その後、音速の単位にもなったエルンスト・マッハ(Wenzel Mach 1838-1916)や「クラインの壺」で有名なフェリックス・クライン(Felix Klein 1849-1925)の元で研究し、1899年に「ピックの定理」を発表したという。その「ピックの定理」とは……。

頂点が格子点にある多角形の面積、Sは、その多角形内部にある点の数、Iと、辺上にある点の数を Bとすると、
S=I+(B/2)-1
と表すことができる。

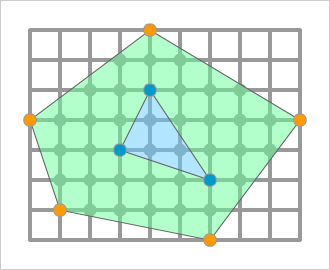
「ピックの定理」を今回の問題に当てはめると、
多角形の内部にある格子点の数、I=37
多角形の辺上にある格子点の数、B=5
S=37+(5/2)-1=38.5
池の内部にある格子点の数、I=3
池の辺上にある格子点の数、B=3
S=3+(3/2)-1=3.5
答えは、38.5-3.5=35

　番組では「ピックの定理」を導出する方法を紹介していた。興味のある人は、Wikipediaの「ピックの定理」の項目を参照してほしい。

　また、いろんな多角形を描いて自分で確かめたい人は、「数学の部屋」の「ピックの定理」にプログラムが掲載されている。

　同じ「数学の部屋」に、多角形の内部に空洞(穴)がある場合の面積を求める式も紹介されている。

内部の点の数を　I
周上の点の数を　B
穴の数を　Hとすると、

空洞多角形の面積 Sは、
S=I+(B/2)+H-1
で表すことができる。

今回の問題に当てはめると、
内部の点の数は、37-(池の周上(3)+池の内部(3))=31
周上の点の数は、街の周上の点(5)+池の周上の点(3)=8
S=31+(8/2)+1-1
S=35

≪参照≫
■数学の部屋
http://web2.incl.ne.jp/yaoki/index.htm
■数学の部屋：ピックの定理
http://web2.incl.ne.jp/yaoki/k12.htm
■数学の部屋：『Pick’s Theorem with Holes』
http://web2.incl.ne.jp/yaoki/pick2.htm