「コマネチ大学数学科56講:ニュートン」の「だんご3兄弟」の問題では、木下眞二さんの完全解答が紹介された。その木下眞二さんから記事へのコメントをいただいた。
他にも、私の創作パズルが、ホームページに載っているので参考にしてください。
とくに、「ゼロの誕生」は、「問題は簡単」「解答は難解」で、私の傑作と思っています。
というわけで、少し時間に余裕ができたので、木下眞二さんのホームページに掲載されている、「ゼロの誕生」問題に挑戦してみた。
まず、ルールを確認しておこう。「0を含まない数を2乗して、その桁数と同じまたはそれ以上の数の0が連続して現れるものを求めなさい」
たとえば、3桁の「100」の2乗は「10000」になり、4つの「0」が連続するが、元の数に「0」を含んでいるので、これはダメ。また「99999」の2乗は「9999800001」になり、4つの「0」が連続するが、元の数の桁数が5桁なので、残念ながら「0」が1つ足りない。もし、これを可とすると、桁数を増やせば、いくらでも「0」が連続する数を作り出すことができてしまう。
手始めに4桁の整数でトライ!
4桁の数では1秒もかからない。ちなみに、使用しているのは1フレームのみで、「計算開始」のボタンが押されたとき、ボタンに記述した以下のスクリプトを実行する。
この(var N=1111; N<9999; N++)のNの桁数を増やせば、4桁以上の数についても、計算できそうな気がする。
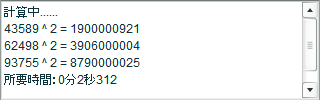
5桁の数では2秒ちょっとかかった。ところが、桁数を6にすると……。

「for~next」でループするとき、あまり時間がかかると、Flashが警告を出す。無視すると、なんとか計算結果は出るが、この方法では、これが限界のようだ。
そこで「計算開始」のボタンが押されたら、2フレームへ飛び、3フレームに入ったら「gotoAndPlay(2)」のように、タイムライン上でループする方法に切り替えた。
わかっていたことだけど、お…遅い;;5桁の計算をするのに12分くらいかかる。Flashでは、フレームレート(実行速度)を「120fps」までしか設定できない。1秒間に120フレームだ。実際に計算をしているのは第2フレームなので、1秒間に60回程度しか計算ができないことになる。桁数を1つ増やすと、単純に計算時間は10倍かかる。つまり、6桁の数だと、12分の10倍で120分。2時間だ><;(※8月25日追記:実際にブログにアップしたFlashで計測したら、20数分かかった。ローカルのプレビューとの差だと思う。)
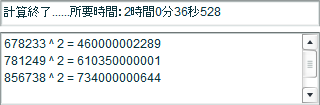
いくら、がまん強い人でも2時間は待ってくれないだろうから、6桁のFlashは掲載をあきらめた。このスクリプトでは、単純にNを1つずつ増やし、元の数Nに「0」が含まれているときは計算しないようにしているが、たとえば、Nが「300000」のように「0」が並んだときは、どうせ除外されるので「N=N+11111」として、計算方法を工夫することが考えられる。これだけで、1万ループぶんは、時間を節約できるわけだ。もっとも、スピードを追求するなら、Flashを使ってどーする……みたいな、根本に立ち戻ってしまう^^;そんなわけで、私には、これが限界だ。
もしも、時間がいくらかかってもよいというのなら、7桁で20時間、8桁で200時間……という調子で、10桁では2万時間(2年4ヶ月ぐらい)で結果が出ると思う。
ちなみに、木下眞二さんのホームページでは、
63597152451976967425497457156971514344785895719391237
848289452254697の2乗、
40445978000000000000000000000000000000000000000000000
00000000000000000000000388010374103983243462524801112
700342822586951861176958561809
……という68桁の解答が載っている。これまで報告されている解答数は81個で、推定される残りの解答は8個とのこと。すべての解答を求めるには、10^24年くらいかかるそうで、計算方法を工夫して効率アップをはかっても、宇宙誕生から現在までと同じほどの時間がかかるらしい。

私の数学パズル「ゼロの誕生」を紹介していだだき、ありがとうございます。
このパズルの解答に協力していただいた人たちの、詳細な解答方法については、「数学文化」の最近号No.8: 73-78 に、東京理科大学の後藤丈志さんが掲載していますので、参照してください。
後藤さんは、このパズルの最大の解答、68桁の2乗を求めた方です。
木下眞二