■コマネチ大学数学科53講：数学オリンピック

2014年冬季オリンピック開催地はロシアのソチに決定した。韓国の平昌(ピョンチャン)は、2010年の冬季オリンピックに続き、またしても決選投票で涙を飲む結果となった。そんな国際オリンピック委員会(IOC)とは、まったく関係のない「たけしのコマネチ大学数学科」の第53講。今回のお題は、2001年国際数学オリンピック(IMO)の予選問題。

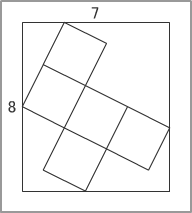問題：縦が8、横が7の長方形の中に図のように5つの合同な正方形が詰め込まれている。正方形の1辺の長さを求めよ。

コマ大数学研究会は、強力な助っ人を求め、マス1グランプリの初代王者、西本さんを待ち伏せ（テロップでは、西本正樹となっていたけれど、西本将樹の間違い？）。でも、助っ人にはなってもらえず＞＜； ちなみに、この問題、西本さんは、わずか49秒で正解した。

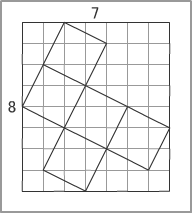戸部アナが「マス北野がマス目を引いています」と思いつきギャグで顰蹙(ひんしゅく)を買ったが、この問題、マス目を引けば、ピタゴラスの定理(三平方の定理)で「1:2:√5」になることは、一目瞭然なのだが……。

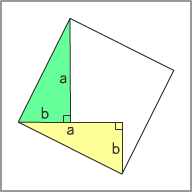そんなわけで、さっそく中村亨センセの「美しき数学の時間」。5つの合同な正方形のひとつを抜き出して、これをグラフのx成分、y成分に分けて考える。

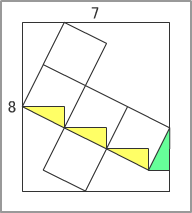x成分は、図のようになり、7=3a+b

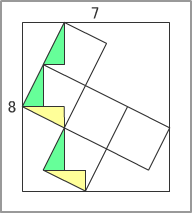y成分は、8=3a+2bになる。

この連立方程式、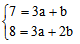


を解くと、(a,b)=(2,1)になるので、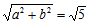


というわけだ。

この問題、2001年数学オリンピックの予選問題ということで、下記の書籍に収録されている。巻末には、IMOにおける日本選手の成績も掲載されていて、西本さん(当時、灘高)は、第44回日本大会(2003年)と第45回ギリシア大会(2004年)で個人タイトルの金メダルをダブル受賞している。

数学オリンピック2000‐2005 (財)数学オリンピック財団／編 発行：日本評論社 価格：2100円＋税 発行年月：2005年10月 ISBN：4-535-78453-1