竹内センセのブログ「薫日記」でも紹介されていたけれど、「インド式計算ドリル」がベストセラーになっているという、中村亨センセの「コマネチ大学数学科」第45講。お題は「軌跡」だよ。

問題:1辺が6cmの正方形の中にコンパスを使い、図のような図形を描く。この図形を直線上で1回転させたとき、図形が通った軌跡の面積を求めよ。
これが、ルーローの三角形ならば、以下のようになるのだが……。
このFlashムービーは、あとで紹介する「GRAPES」というフリーソフトのサンプルを連続保存して、それをFlashのタイムラインに貼り付けたもの。
ルーローの三角形は、以前のエントリ「コマネチ大学数学科」の第13講「ソファー問題」でも、紹介したことがある。ルーローの三角形が動く軌跡は、高さが一定の長方形になる。しかし、今回の問題は、ルーローの三角形とよく似ているが、ハート型となっている(このへんが一筋縄ではいかない中村亨センセのなせる業^^)。直線上を転がりながら動く軌跡を見ると、ルーローの三角形とほぼ同じだが、途中で妙な動きをする。
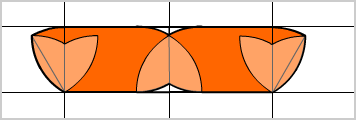
今回の問題は、この不規則な動きをする軌跡の面積を求めることがポイントになる。
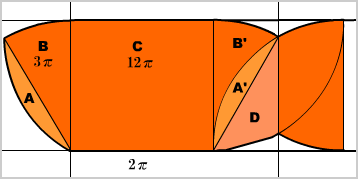
1回転するということは、半回転したときの面積を求め、それを倍にすればいい。Bの部分の面積は、円の面積(πr^2)の30度分なので、π*(6*6)*(30/360)で、3π。B’の部分も同様。Cの部分は、π*(6*6)*(120/360)で、12πになることは、すぐにわかる。
問題は、AとDの部分だが、AをA’に移動させると、レンズ型の図形の1/2になっていることがわかる。つまり、A+Dの面積は、((πr^2)/4)-((r^2)/2))で、rに6cmを代入すると、(π*6*6*(90/360))-(6*6/2)=9π-18になる。
(A+B+B’+C+D)の2倍が軌跡の面積なので、(27π-18)*2、(27*3.14-18)*2=約134平方cmとなる。
なんか、もっと、あっと驚く考え方があるのかと思ったら、地道に計算するしか、方法はないようだ。ルーローの三角形の軌跡の面積から、スキマを引くという考え方もあるが、結局は、計算で求めるしかない。マス北野も途中までは計算していたが、計算が面倒になり、あきらめてしまった。結局、地道に計算をした東大生チームがフィールズ賞を勝ち獲った。
この記事の冒頭にあるFlashムービーは、「GRAPES」というフリーウェアのソフトを使って作成した。世の中には、こういった有用なソフトを作成し、それを無料で公開している人もいる。感謝すると同時に、インターネットってすばらしいなぁと思う。私自身は、このソフトを使いこなしているとは、とても、言えないけれど……。
■WelCome to GRAPES(GRAPES 6.51ダウンロード可)
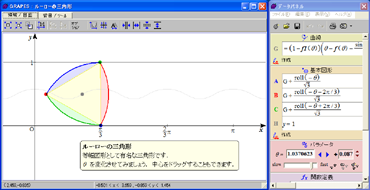
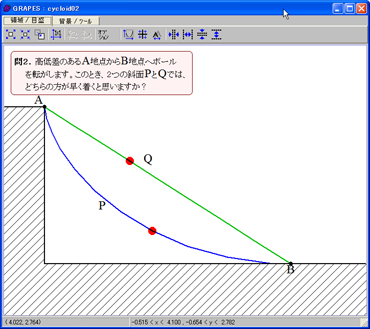
「GRAPES」を使ったサンプル集で、中村亨センセが番組内で紹介した、サイクロイド曲線を転がる玉の問題も、このサイトでダウンロード可能だ。
「GRAPES」の関連書籍のアフィリエイト
 パソコンらくらく高校数学図形と方程式 ―関数グラフソフト「GRAPES」で図形の性質を簡単マスター 著者:友田 勝久,堀部 和経 |

コマネチ大学 #45
コマネチ大学 #45
たけしのコマネチ大学#45 2007/05/10 深夜OA
今回のテーマは、
「軌跡」
◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇
英語で言うと、a Locus。
点が一定の条件に従って動くときに描く図形のことなんです…
grapesでルーローの三角形を動かしたいので、パラメータ等サンプルがあればいただきたいのですが。まさに45講にあるものがいいのですが。
マツダ命さま、コメントありがとうございます。
記事にもあるとおり、ルーローの三角形は「GRAPES」のサンプルを使わせていただきました。「GRAPES」を起動し、「ファイル」メニューの「サンプルを開く」から、「幾何」フォルダにある「ルーローの三角形.gps」を開くと表示されます。
画像を動かすには「ファイル」メニューの「画像の連続保存」を選びます。保存先のフォルダを指定すると、そこにBMP形式で保存されます。私の場合は、連続する画像をFlashに貼り付けたわけですが、アニメーションGIFでも実現できると思います。
お名前から判断して「ロータリーエンジン」に興味があるなら、「第13回:ソファー問題」で紹介させていただいた「式から求めるトロコイド曲線 ~オニギリ・ジョーPresents~」のサイトがおすすめです。このブログの右上にある「サイト内検索」で「ロータリー」で検索してみてください。
ありがとうございます。
使わせていただきます。