昨年末の「M-1グランプリ」は「チュートリアル」が獲ったけれど、もう一つの「M-1」、「マス1グランプリ」は誰の手にと楽しみにしていた「コマネチ大学数学科マス1グランプリ」。期待に違わず、かなり楽しめた。しかし、「いいちこ」漬けの頭では、リアルタイムに参戦できるわけもなく、録画した番組であらためて問題を振りかえってみた。
●ROUND1 計算問題

計算すれば答えは出るのだけれど、いかに式を簡単にするのかがポイント。私がパッと答えることができたのは、問9だけだった;;
●ROUND2 最速図形バトル
計算問題で出遅れたマス北野だったが、さすがに図形問題では最速。しかも、上のFlashで紹介している解法は、ハサミを4回入れなければならないが、マス北野は、たった2回ハサミを入れるだけで、正解した。じつは、2番目に速かったのは、西本さん。しかし、思考速度は速いものの、不器用ぶりを発揮し、図形を並び替えることに手間どり、東大生チームに先を越されてしまった。ツッコミどころも満載の西本さんであった。
●FINAL ROUND 一騎打ちバトルロイヤル
マス北野と数学オリンピックの2年連続チャンピオン、西本さんとの一騎打ちとなった。
問題は「1000本の棒を使って正四面体を作り、積んでいくと、何段になるでしょう?」というもの。ひとつの正四面体を作るには、6本の棒が必要。これを1000本以内で、図のように積み上げていくと、何段作ることができるかということ。

1段目は正四面体が1個。2段目は3個。3段目は6個……と続く。関係ないが、「Shade」で正四面体を描くことが、こんなに大変だとは思わなかった。で、1つの正四面体を描いたなら、あとは、コピーして貼り付けるだけなのだが、これも、意外とめんどうくさい。2段目で挫折……。それを考えると、コマ大数学研究会のがんばりは、スゴイ!と思う。
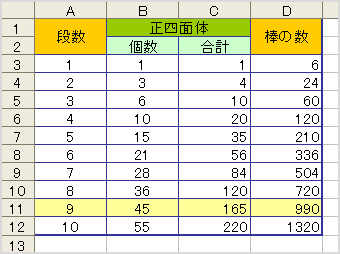
というわけで、エクセルで表にしてみた。段ごとの正四面体の数は、1段目からその段までの数を足したものになる。セルB4に「=SUM($A$3:A4)」として、オートフィルで以下の行を連続入力する。合計の欄も同じく、セルC4に「=SUM($B$3:B4)」とする。この合計に6を掛ければ、棒の数が出る。9段目で990本になり、10段目では1000本を超えてしまう。
これは、マス北野の方法と同じだ。西本さんは、最速ですぐにこの問題を解く公式を導き出した。ただ、番組では説明の部分がカットされていたのが残念だ。
美しき数学の時間では、竹内薫センセが解説。この問題、パスカルの三角形を用いても解くことが可能とのこと。
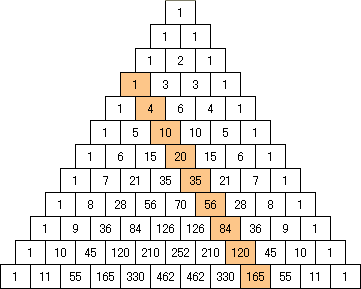
正四面体の合計数が表れているではないか。しかも上から数えてみると、9段目が「165」になる。まるで、手品で「引いたカードをあらかじめ予言しておきました」みたいな、パスカルの三角形。パスカル、あんたはスゴイ! ふと、今、思いついたのだけれど「同じ大きさの鏡餅を3つ並べて、その上に1個置く。このような形で10段の鏡餅を作るには、鏡餅は何個必要ですか?」という、お正月らしい問題ならば、コマ大数学研究会は、これほど苦労しなかったはず……あ、これじゃ、番組として成り立たないのか^^;
でも、段ごとに必要な正四面体の数を考えるとき、鏡餅で考えると、わかりやすいかもよ。

いつも応援ありがとうございます!
問題解説は、番組よりもガスコン研究所のほうが上ですね(汗)
Shadeやエクセルといった道具も面白いです。
放送もあと残り3ヶ月となりましたが、どうか、最後までヨロシク!
新年早々、ごめんなさいです。昨年もやらかしてしまいましたが、薫日記に同じトラックバックを二度送ってしまいました。記事を公開したときに文章上の誤りを見つけ、それを修正して再度、アップした際にトラックバック欄にまだ残っているのを確認しなかったのです。トラックバックスパムとも受け取れるようなミスです。竹内薫センセ、お手数をおかけし、申し訳ありませんでした。
本年も、問題の作成は大変でしょうけれど、数学の面白さ、楽しさを味わせてください。そして「美しき数学の時間」での驚きの解説を期待しています。
タメになるし、刺激的な深夜番組 「コマネチ大学数学科」
昨年から録画してでも観ている唯一の深夜番組が、たけしが主演する「コマネチ大学数学科」。
今さらですが、はっきりいってオススメ。
3月までの放映らしいので、今からでも観て欲しい!
質が高くも、ある程度の算数の力(数学でない)の力さえあれば工夫次第で解ける良問が出題されるところが最大のオススメポイント(暗算でも回答可)。
さて先日、M-1グランプリ(M-1のMはMathmaticsのM)なるものが開催され、真の数学王が決定した。
優勝…
この回で、積み重ねた立方体の表面に色を付けたとき、この色を付けた面の数と色が付いていない面が等しくなるときの立方体の個数を求める問題が有りました。 この番組の録画を失敗しました。正解の求め方は自力では解けません。解き方をご教授ください。よろしくお願い致します。
コマネチ大学 #32 SP 問題
理科系の私が眠い目をこすりながら毎週見ているのがたけしのコマネチ大学である。(01/04/2007 深夜OA)
今年の一回目は1時間スペシャルで内容も軽めで面白かったので紹介したい。
第一ステージは、問題10問を制限時間(10分ぐらい)で解くもの。早くできたものから高得点と…
コマネチ大学 #32 SP 解答
たけしのコマネチ大学 正月SP の解答は、問題の記事の下につくるようにしました。
こちらから飛べます。
問題文はこちら
ステージ1の解答
(UPしました)
ステージ2の解答
(UPしました)
ステージ3の解答
(UPしました)
まぁ読んでみてください。…